Хелпикс

Главная

Контакты

Случайная статья



Тест по теме: «Первообразная и интеграл»



Тест по теме: «Первообразная и интеграл»

В заданиях 1-5 записать только номер ответа, в заданиях 6-10 записать решение

1. Определите функцию, для которой F(x) = x2 – sin2x – 1 является первообразной:

1) f(x) = ;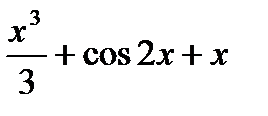

 2) f(x) = 2x – 2cos2x;

3) f(x) = 2x + 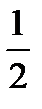cos2x; 

4) f(x) = 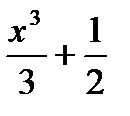cos2x + x.

2. Найдите первообразную для функции. f (x) = 4х3 + cos x

1) F(x) = 12x2 – 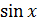+ c;  

 2) F(x) = 4x3 + 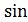x + c; 

3) F(x) = x4 – 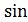x + c;

4) F(x) = x4 + 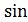x + c.

3. Для функции f(x) = х2 найдите первообразную F, принимающую заданное значение в заданной точке F (- 1) = 2.

1) F(x) = ;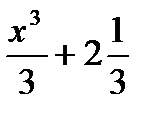    

 2) F(x) = 2x + ;   

 3) F(x) = – ;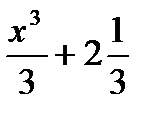  

 4) F(x) = .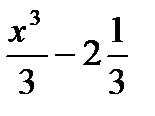

4. Точка движется по прямой так, что её скорость в момент времени t равна v (t) = t + t2. Найдите путь, пройденный точкой за время от 1 до 3 сек, если скорость измеряется в м /сек.                       

   1) 18 м;       2) 12 м;      3) 17 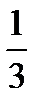м;      4) 20 м.

5. Вычислите  .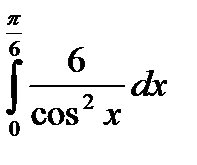                    

1) 6 ;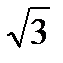      

 2) 6;       

3) 2 ;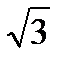     

4) 3 .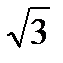

6. Найдите площадь криволинейной трапеции, ограниченной линиями:

 у = – х2 + 3 и у = 0.

1) 4 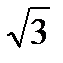;      2) 6 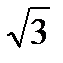;     3) 9 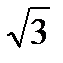;    4) 8 .

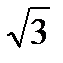7. Найдите площадь фигуры, ограниченной линиями у =   и у = х.

  1) 2;        2) 1 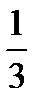;          3) 2 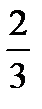;         4) 1 .

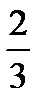8. Вычислите  .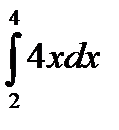       

9.     Найдите сумму абсцисс точек пересечения графиков функции

   у = (х – 1)(х + 2) и её первообразной, если одна из этих точек находится на оси ординат.

10. Найдите ту первообразную функции f(x) = 3х – 1, для которой уравнение F(x) = 5 имеет единственный корень.
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.