Тригонометрические функции y= tgx, y=ctgx

Тригонометрические функции y= tgx, y=ctgx

Рекомендую видео урок по ссылке

https://cknow.ru/knowbase/696-335-trigonometricheskie-funkcii-ih-grafiki.html

Тангенс

График функции:

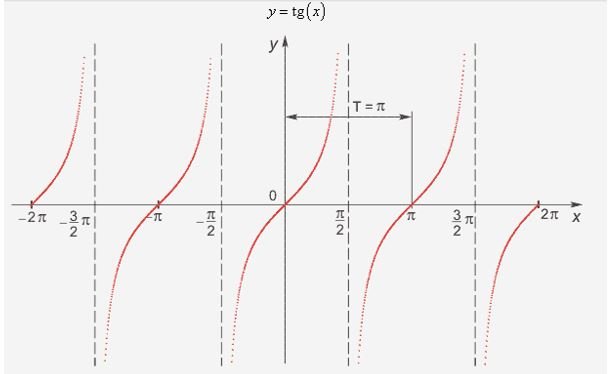
1. Так как тангенс - это отношение синуса к косинусу, то косинус не может быть равен нулю. А давайте вспомним, при каком значении аргумента косинус равен нулю? При π/2.

Это значит, что функция определяется на всем множестве действительных чисел, кроме π/2 и 3π/2.

2. Функция может иметь любое значение из множества действительных чисел.

3. Функция равна нулю при х = 0, функция больше нуля для х ϵ (0; π/2), функция отрицательна при х ϵ (-π/2; 0), все описанные промежутки повторяются с периодом в π.

4. Функция возрастает на всех рассматриваемых промежутках.

Котангенс

График функции:

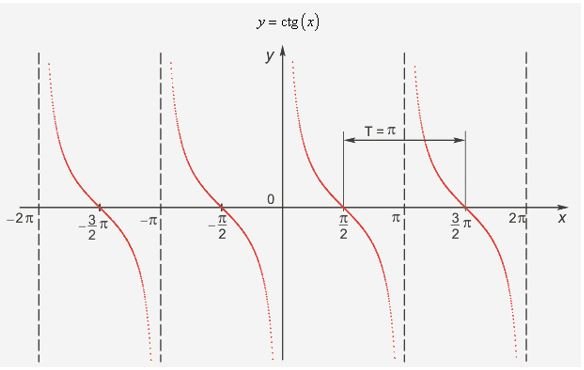
1. Так как котангенс - это отношение косинуса к синусу, то синус не может быть равен нулю. А давайте вспомним, при каком значении аргумента косинус равен нулю? При 0 и π.

Это значит, что функция определяется на всем множестве действительных чисел, кроме 0 и π.

2. Функция может иметь любое значение из множества действительных чисел.

3. Функция равна нулю при х = π/2, функция больше нуля для х ϵ (-π/2; 0), функция отрицательна при х ϵ (0; π/2), все описанные промежутки повторяются с периодом в π.

4. Функция убывает на всех рассматриваемых промежутках.