
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Нахождение % отношения разности двух данных чисел к одному из них.
Решение задач на проценты
Процент - сотая часть числа.
Рассмотрим первый вид задач на проценты - Задачи на нахождение процентов числа. Для их решения важно выделить число, от которого рассматриваются проценты, уметь находить 1 или несколько процентов числа.
Чтобы найти 1% от числа достаточно число разделить на 100.
Деление числа на 100 можно заменить умножением на 0,01.
Найдите чему равен 1% метра; 1% рубля; 1% от 500; 1% от 20.
(1 см; 1 коп.; 5; 0,2)
Чтобы найти несколько процентов числа достаточно число разделить на 100 и умножить на число процентов.
Найдите сколько см составляют 5%; 50%; 20% от метра.
| 100 см: 100 = 1 см | 100 см: 100 = 1 см | 100 см: 100 = 1 см |
| 1 см ×5= 5 см | 1см ×50 = 50 см | 1см ×20= 20 см |
В решении задач этого вида помогают графические иллюстрации.
Задачи на нахождение процентов числа
Зад.1
В школе 800 учащихся. 9% всех учащихся - отличники. Сколько в школе отличников?
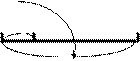 9%
х 9%
х
| 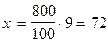 (уч-ся) (уч-ся)
|
| 800 уч-ся |
Зад 2
Завод должен выпустить по плану 800 тракторов. Он выполнил план на 108%. Сколько тракторов выпустил завод?
108%
 х
х
| |
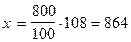 (трактора) (трактора)
| |
| 800 тр. |
Зад.3
1 метр материи стоит 50 руб. Цена снизилась на 15%. На сколько рублей дешевле стал стоить 1 метр материи?
 15% 15%
| |
| х | 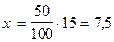 (руб) (руб)
|
| 50 руб |
Зад.4
Фермер наметил занять 120 га кукурузой, а засеял кукурузой площадь на 5% большую. На сколько га больше засеял фермер кукурузой, чем намеревался первоначально?
 5% 5%
| |
| х | 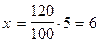 (га) (га)
|
| 120 га |
Второй вид задач на проценты - задачи на нахождение числа по его процентам. Как же найти число, зная 1 или несколько его процентов?
Чтобы найти число, если известно чему равен 1% его, достаточно число, которое составляет 1%, умножить на 100.
Найдите число, 1% которого равен 6,2; 1% которого равен 3.(6,2×100 = 620; 3× 100 = 300)
Чтобы найти число по его нескольким процентам, достаточно число, которое составляет несколько процентов, разделить на число процентов и умножить на 100.
Найдите число, 2% которого составляют 2 см; 2% которого составляют 6 коп.
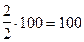 (см) (см)
| 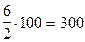 (коп) (коп)
|
Для решения этих задач, они являются обратными для задач 1-4 также используют графические иллюстрации.
Задачи на нахождение числа по его процентам
Зад.5
В школе 72 отличника, что составляет 9% всех учащихся. Сколько в школе учащихся?
72 уч-ся
 9%
х 9%
х
| 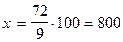 (уч-ся) (уч-ся)
|
Зад.6
Завод выпустил 864 трактора, выполнив план на 108%. Сколько тракторов должен был выпустить завод по плану?
 108%
864 тр. 108%
864 тр.
| |
| х | 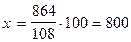 (тр.) (тр.)
|
Зад.7
После очередного снижения цен на материю на 15% 1 метр ткани стал стоить на 7,5 рублей дешевле. Сколько стоил 1 метр ткани до снижения?
 15%
7,5 руб 15%
7,5 руб
| |
| х | 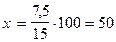 (руб) (руб)
|
Зад.8
Фермер засеял кукурузой на 6 га больше, чем намечал, тем самым занял на 5% большую площадь. Сколько гектаров наметил фермер первоначально засеять кукурузой?
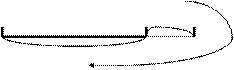 5% 5%
| |
| 6 га | 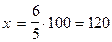 (га) (га)
|
| х |
Третий вид задач на проценты - задачи на нахождение процентного отношения двух чисел.
Обратимся к конкретной задаче: Ученику надо прочитать книгу, которая содержит 300 страниц, а он успел прочитать только 250 страниц. Какую часть книги он прочитал?
Для ответа на вопрос задачи находят отношение числа прочитанный страниц к числу страниц, которые надо прочитать: 250 : 300 = 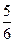
Чтобы найти, какую часть одно число составляет от другого, надо записать в виде дроби частное от деления первого числа на второе.
Часто это отношение выражают в процентах. Обратимся к задаче: Рабочему надо изготовить за смену 400 деталей. До обеда он сделал 300 деталей. Какую часть нормы рабочий выполнил до обеда? Какой процент нормы он выполнил до обеда?
300 : 400 = 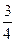 ; ;
| 400 деталей составляют 100% на 1% приходится 400:100=4 (дет.) 300 : 4 = 75 (%) |
| или сразу находят отношение двух чисел в процентах | 300 : 400 × 100 = 75 (%) или
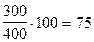 (%) (%)
|
Задачи на нахождение процентного отношения двух чисел являются обратными по отношению к задачам как первого, так и второго видов. В их решении также полезно использовать графические иллюстрации.
Задачи на нахождение процентного отношения двух чисел
Зад.9
Из 800 учащихся школы 72 ученика - отличники. Какой процент всех учащихся школы составляют отличники?
 х% х%
| |
| 72 уч-ся | 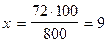 (%) (%)
|
| 800 уч-ся |
Зад.10
Завод выпустил 864 трактора вместо 800 по плану. На сколько процентов завод перевыполнил план?
х%
 864 тр.
864 тр.
| |
| 800 тр. | 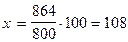 (%) (%)
|
Зад.11
1 метр материи стоил 50 рублей. После снижения цен он стал стоить на 7,5 рублей дешевле. На сколько процентов снизилась цена?
 х% х%
| |
| 7,5 руб | 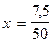 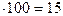 (%) (%)
|
| 50 руб |
Зад.12
Фермер наметил засеять кукурузой 120 гектаров, а засеял на 6 га больше. На сколько процентов больше он занял площадь под кукурузу, чем намечал?
 х% х%
| |
| 6 га | 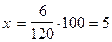 (%) (%)
|
| 120 га |
Эти три вида задач относятся к простейшим задачам на проценты.
Простейшие задачи на проценты
Задача 1.
Урожай кукурузы составил 665 центнеров с гектара, а урожай подсолнечника 97% от этого количества. Сколько в среднем сняли с 1 га посевов подсолнечника?
Задача 2.
Никелевая сталь содержит 3,4% чистого никеля. Сколько чистого никеля содержится в 1500 кг никелевой стали?
Задача 3.
На ферме 760 свиней, что составляет 190% от поголовья прошлого года. Сколько свиней было на ферме в прошлом году?
Задача 4.
Территория города 34000 га. Общая площадь лесных насаждений в городе равна 5787 га. Сколько процентов городской территории занимают лесные насаждения?
Задача 5.
Совхоз должен был засеять зерновыми по плану 1680 га. Было засеяно на 280 га больше. На сколько процентов совхоз перевыполнил план?
Задача 6.
Ученик, проходя практику, изготовил за смену 36 деталей, что составляет 72% нормы. Сколько деталей нужно изготовить по норме?
Задача 7.
Картофель содержит 20% крахмала. Сколько картофеля нужно для получения 12 кг крахмала?
Задача 9.
Для определения влажности зерна берут навеску в 5 г, тщательно сушат и снова взвешивают. Определить процент влажности, если после сушки зерно весило 4,25 г
Задача 10.
Человек может почувствовать изменение массы предмета, который он держит в руке, если это изменение будет не менее 3% массы предмета. Какое наименьшее количество граммов нужно добавить к гире в 500 г, чтобы человек почувствовал изменение массы?
Задача 11.
Сколько нужно взять воды, чтобы приготовить из 200 г соли 5-процентный раствор?
Задача 12.
После снижения цен 1 м материи стал стоить на 12 руб. дешевле. Найти цену одного метра ткани до и после снижения цен, если цены снизились на 15%.
Нахождение % отношения разности двух данных чисел к одному из них.
Задача 1.
В группе 25 девочек и 20 мальчиков. На сколько процентов мальчиков меньше, чем девочек?
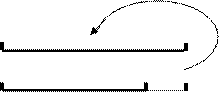
|
25 дев.
х%
20 мальч. | ||
| 1)25-20=5 (чел.) 2)(5:25)·100 = 20(%) | 1)(20:25) ·100=80(%) 2) 100-80= 20(%) |
Задача 2.
В группе 25 девочек и 20 мальчиков. На сколько процентов девочек больше, чем мальчиков?
|
25 дев. х% | 1) 25-20=5 (чел.) | 1) (25:20) ·100 = 125(%) |
| 2) (5:20)·100 = 25(%) | 2) 125- 100= 25(%) |
20 мальч.
Задача 3.
Число уменьшилось на 20%. На сколько процентов нужно увеличить новое число, чтобы получить первоначальное?
x
20% y z%
| 1) 100-20=80 (%) составляет новое число от первоначального | |||
| 2) (20:80) · 100= 25(%) |
Задача 4.
Число увеличилось на 25 %. На сколько процентов нужно уменьшить полученное число, чтобы вновь получить данное?
|
25% z%
y | 1) 100+25=125 (%) составляет новое число от первоначального |
| 2) (25:125) · 100= 20 (%) |
На примере данных задач становится понятным, что при решении задач на проценты важно учитывать, с каким числом идет сравнение, какое число принято за 100%. По ходу решения задачи то, что принимается за 100%, может меняться. В ряде задач следует учитывать, какое данное по ходу задачи остается неизменным. Так при сушке фруктов или грибов, как правило неизменным по массе остается абсолютно сухое вещество и т.п.
Более сложные задачи на проценты:
Задача 1.
Имеется два сосуда, содержащих 4 кг и 6 кг раствора кислоты разных концентраций. Если их слить вместе, то получится раствор, содержащий 35% кислоты. Если же слить равные массы этих растворов, то получится раствор, содержащий 36% кислоты. Сколько килограммов кислоты содержится в каждом сосуде?
Задача 2.
Свежие грибы содержат по массе 90% воды, а сухие – 12%. Сколько получится сухих грибов из 11 кг свежих грибов? Сколько килограммов свежих грибов надо собрать, чтобы получить 1 кг сухих?
Задача 3.
Древесина только что срубленного дерева содержит 64% влаги, а через неделю только 48% влаги. На сколько уменьшится масса бревна в 7,5 центнеров за эту неделю?
Задача 4.
В только что добытом каменном угле содержится 2% воды. Через два дня уже 12% воды. На сколько увеличится масса центнера добытого угля за эти два дня?
Задача 5.
При поставке картофеля по договору с хозяйством может быть 20% мелкого, в доставленной партии в 12,5 тонн было 24% мелкого картофеля. Сколько тонн крупного картофеля следует добавить, чтобы выполнить договорное обязательство?
Задача 6.
Стоимость изделия удалось снизить сначала на 10%, а через месяц еще на 15% с новой стоимости. На сколько процентов снизилась стоимость изделия в результате двух снижений?
Задача 7.
До просушки влажность зерна была равна 23%, а после просушки оказалась равной 12%. На сколько процентов уменьшилась масса зерна в результате просушки?
Задача 8.
Свежие фрукты содержат 72% воды, а сухие – 20% воды. Сколько сухих фруктов получится из 20 кг свежих?
Задача 9.
Производительность труда рабочего повысилась на 20%. На сколько процентов уменьшится время, необходимое для выполнения одной и той же работы?
Задача 10.
Скорость движения поездов на данном участке пути увеличили на 25%. На сколько процентов уменьшилось время, необходимое для прохождения этого участка пути?
Задача 11.
Сколько граммов воды нужно добавить к 150 г 75% -го раствора, чтобы получить 25%-й раствор?
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
 х
х