Перестановки. Пример 3.. Размещения

Перестановки

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Перестановками называются такие выборки элементов, которые отличаются только порядком расположения элементов, но не самими элементами.

Если перестановки производятся на множестве из n элементов, их число определяется по формуле

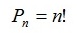
Пример 3.

Сколько можно составить четырехбуквенных «слов» из букв слова «брак»?

Решение

Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.

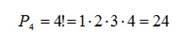
Размещения

Классической задачей комбинаторики является задача о числе размещений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

Размещениями из n элементов по m (мест) называются такие выборки, которые имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения.

Число размещений изnпоm обозначается A_n^m и определяется по формуле

⇐ Предыдущая 1 234 Следующая ⇒