Если переменная = 0 или 1, то среднее совпадает с долей.

Задача 2

Ваня любит пить чай. Иногда он пьёт его с сахаром, иногда без. На этой неделе он помечал цифрой 1 дни, когда пил чай с сахаром. Получилось 1, 1, 0, 0, 1, 0.

а) Найдите среднее значение сахарных дней в жизни Вани. Найдите дисперсию сахарных дней.

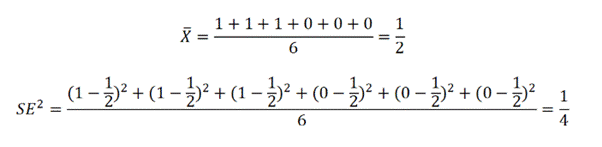
б) Правда ли, что среднее число сахарныхдней совпало с долей сахарных дней? Почему так вышло? Всегда ли так будет происходить?

Доля сахарных дней =Количество сахарных дней / Количество всех дней

Доля сахарных дней = Среднее

Если переменная = 0 или 1, то среднее совпадает с долей.

в) Между дисперсией и долей в случаях, когда переменная принимает значения 0 или 1 тоже есть связь. Сможете догадаться как будет выглядеть формула, описывающая эту связь?

𝑆𝐸^2=𝑝(1−𝑝)

где p – доля единиц

!Формула только если переменные 0 и 1!

Задача 2

Имеется пять чисел: x, 9, 5, 4, 7. При каком значении x медиана будет равна среднему? А можно ли поставить такие цифры в условии задачи, чтобы x не существовал?

Для начала располагаем всё в порядке возрастания:

4, 5, 7, 9

А теперь думаем: в зависимости от того, где в этом ряду стоит х у нас будет меняться медиана. Если х мы поставим перед 5, то 5 становится медианой. Если же ставим сразу после 5, то медианой становится сам х. А если же после 7, то медианой будет 7.

Составляем уравнения, где среднее = медиана:

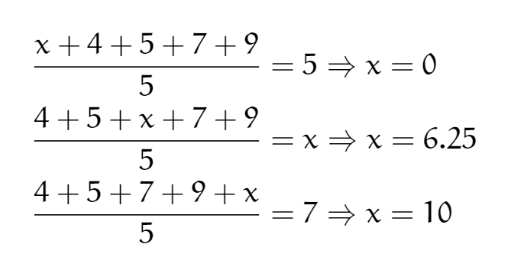
Задача 4

Измерен рост 25 человек. Средний рост оказался равным 160 см. Медиана оказалась равной 155 см. Машин рост в 163 см был ошибочно внесен как 173 см. Как изменится медиана и среднее после исправления ошибки? А как могут измениться медиана и среднее, если рост Маши равен 153?

Дано:

n = 25

Средний рост = 160 см

Медиана = 155 см

Если рост Маши 173 —> 163

mean = 160−10/25=159,6

Медиана не изменится, так как и то и другое значение лежит выше середины (155)

Если же её рост 153, то меняется и среднее (аналогично), и медиана.

Задача 8

Пункт 1.

Разберём на примере. У нас есть 8 зарплат, запишем их в ряд.

Первая ситуация:

1 2 2 3 3 4 4 5

med = 3

2/3med = 2

2med = 6

1 [ 2 2 3 3 4 4 5]

В “средний класс” попадает 7 человек.

Вторая ситуация:

0 1 1 2 4 4 5 7

med = 3

2/3med = 2

2med = 6

0 1 1 [ 2 4 4 4 ] 8

В “средний класс” попадают только 4 человека.

Заметим, что общая сумма чисел и даже медиана не изменились, а средний класс всё равно уменьшился. Так почему же это произошло? Всё из-за неравномерного распределения богатств (на примере с зарплатой) или же расслоения. Очень бедных становится больше, а состояние одного очень богатого увеличивается за их счет, а потому первые перестают быть средним классом, так же как и богатый (если он вообще когда-то в нем был) выходит из среднего класса.

Таким образом, медиана не обязательно должна изменяться при изменении уровня дохода. Если изменения происходят по одну сторону медианы, то они “выпадают” из границ ⅔-2, не меняя при этом саму медиану.

Пункт 2

Всё зависит от ситуации.

Например:

0 0 0 1 2 4 5 12

med = 1.5

2/3med = 1

2 med = 3

0 0 0 [1 2 ] 4 5 12 - средний класс

mean = 3

2/3mean = 2

2mean = 6

0 0 0 1 [ 2 4 5 ] 12 - средний класс

Или же

2 3 3 3 3 3 3 12

med = 3

2/3med = 2

2med = 4

[2 3 3 3 3 3 3] 12 - средний класс

mean = 8

2/3mean =~5.3

2mean = 16

2 3 3 3 3 3 3 [12] - средний класс

Как мы видим, всё зависит от среднего отклонения. В первом случае оно равнялось ~3.7, а во втором ~5. Поэтому в первом медиана выдала меньше среднего класса, нежели это сделало “среднее”, а во втором наоборот.

В США используется медиана, так как там очень много “выбросов”. Медиана, в отличие от среднего, к ним не чувствительна.