
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Сфера и шар. Уравнение сферы.
Сфера и шар. Уравнение сферы.
 Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
Данная точка называется центром сферы, а данное расстояние – радиусом сферы.
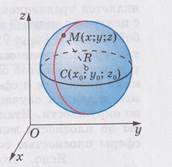 Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также является радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы.
Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также является радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы.
Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются центром, радиусом и диаметром шара.
В прямоугольной системе координат уравнение сферы радиуса R с центром С(x0; y0; z0) имеет вид
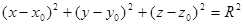
Уравнение сферы с центром в начале системы координат имеет вид: 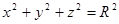 ,
,
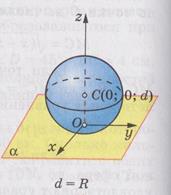
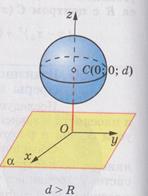
Возможны три вида расположения плоскости и сферы.
1. Если расстояние от центра сферы до плоскости меньше радиуса сферы ( 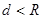 ), то плоскость и сфера пересекаются и сечением сферы плоскостью является окружность.
), то плоскость и сфера пересекаются и сечением сферы плоскостью является окружность.
2. Если расстояние от центра сферы до плоскости равно радиусу сферы ( 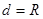 ), то плоскость и сфера имеют только одну общую точку.
), то плоскость и сфера имеют только одну общую точку.
3. Если расстояние от центра сферы до плоскости больше радиуса сферы ( 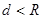 ), то плоскость и сфера не имеют общих точек.
), то плоскость и сфера не имеют общих точек.
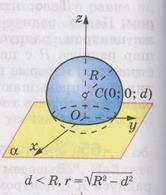
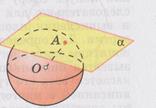 Теорема.Радиус сферы, проведённой в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Теорема.Радиус сферы, проведённой в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Теорема. Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
Площадь сферы равна  .
.
Пример 1.Напишите уравнение сферы радиуса 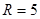 и центром в точке А(2: 5; 9).
и центром в точке А(2: 5; 9).
Решение.
Уравнение сферы имеет вид 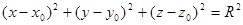 .
.
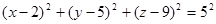 ;
;
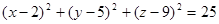 .
.
Ответ: 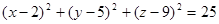 .
.
Пример 2. Найдите площадь поверхности шара радиусом 66 см.
Решение.
Площадь шара равна  .
.
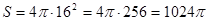 (см2).
(см2).
Ответ: 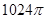 см2.
см2.
Домашнее задание.
№ 576. Напишите уравнение сферы радиуса R с центром в точке А, если:
а) А(2; -4; 7), R = 3; б) А(0; 0; 0), 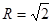 ; в) А(2; 0; 0), R = 4.
; в) А(2; 0; 0), R = 4.
№ 585.Все стороны ромба, диагонали которогоравны 15 см и 20 см, касаются сферы радиуса 10 см. Найдите расстояние от центра сферы до плоскости ромба.
№ 593. Найдите площадь сферы, радиус которой равен: а) 6 см; б) 2 дм; в) 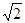 м; г)
м; г) 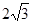 см.
см.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|