
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вологодский государственный университет»
федеральное государственное бюджетное образовательное учреждение высшего образования
«Вологодский государственный университет»
Институт машиностроения энергетики и транспорта
Кафедра «Электрооборудование»
(наименование кафедры)
Дисциплина: «Физика»
Наименование темы:
Шифр работы КР ____________________________________________
код специальности/направления код кафедры регистрационный номер по журналу год
| Руководитель | ст.пр. Мелконян Ш. Р |
| (уч. степень, звание, должность. Ф.И.О) | |
| Выполнил (а) студент | Цыпилев М. В. |
| (Ф.И.О) | |
| Группа, курс | 5Б13-ЭО 15/зу |
| Дата сдачи | |
| Дата защиты | |
| Оценка по защите | |
| (подпись преподавателя) |
Вологда
2020 г.
7. Тело брошено с начальной скоростью с высоты h=2,4 м вверх под углом 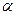 =350 к горизонту и упало на расстоянии l=37 м от места бросания. Найти начальную скорость тела.
=350 к горизонту и упало на расстоянии l=37 м от места бросания. Найти начальную скорость тела.
Дано:
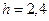 м
м
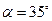
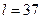 м
м
Найти: 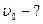
Решение:
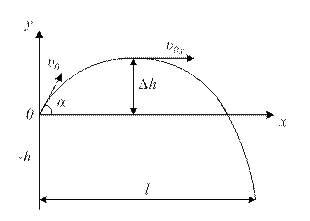
Дальность полета тела: 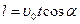 .
.
Уравнение движения тела: 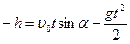 .
.
Тогда 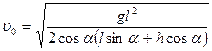 .
.
Находим числовое значение:
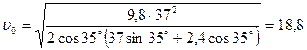 м/с.
м/с.
Ответ: 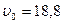 м/с.
м/с.
17. Автомобиль массой m=5000 кг движется со скоростью 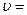 10 м/с по выпуклому мосту. Определить силу давления автомобиля на мост в его верхней точке, если радиус кривизны моста R=50 м.
10 м/с по выпуклому мосту. Определить силу давления автомобиля на мост в его верхней точке, если радиус кривизны моста R=50 м.
Дано:
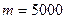 кг
кг
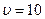 м/с
м/с
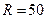 м
м
Найти: 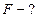
Решение:
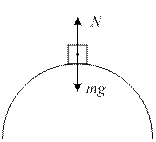
Согласно второму закону Ньютона: 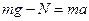 .
.
Тогда 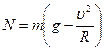 .
.
Откуда 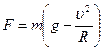 .
.
Находим числовое значение:
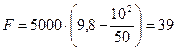 кН.
кН.
Ответ: 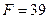 кН.
кН.
27. В деревянный шар массой m1=8 кг, подвешенный на нити длиной l=1,8 м, попадает горизонтально летящая пуля m2=4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в ней пулей отклонилась от вертикали на угол 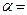 30? Размером шара пренебречь. Удар пули считать прямым, центральным.
30? Размером шара пренебречь. Удар пули считать прямым, центральным.
Дано:
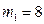 кг
кг
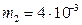 кг
кг
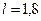 м
м
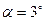
Найти: 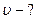
Решение:
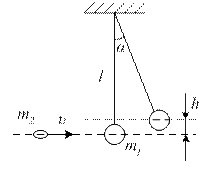
По закону сохранения импульса: 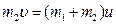 .
.
Согласно закону сохранения энергии: 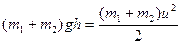 . Тогда
. Тогда 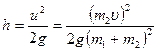 .
.
Учитывая, что 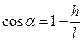 , запишем итоговое выражение
, запишем итоговое выражение 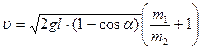 .
.
Находим числовое значение:
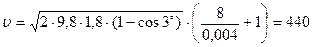 м/с.
м/с.
Ответ: 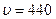 м/с.
м/с.
37. Из шахты глубиной h=600 м поднимают клеть массой m=3 т на канате, каждый метр которого имеет массу m1=1,5 кг. Какая работа совершается при поднятии клети на поверхность Земли? Каков КПД подъемного устройства?
Дано:
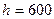 м
м
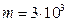 кг
кг
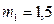 кг
кг
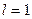 м
м
Найти: 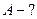 ,
, 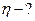
Решение:
Работа по подъему клети: 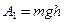 .
.
Работа по подъему каната: 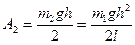 .
.
Тогда полная работа 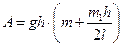 .
.
Коэффициент полезного действия: 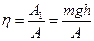 .
.
Находим числовые значения:
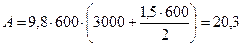 МДж,
МДж,
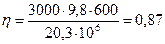 .
.
Ответ: 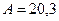 МДж,
МДж, 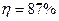 .
.
87. В сосуд льется вода, причем за секунду наливается объем воды 0,2 л. Каким должен быть диаметр отверстия в дне сосуда, чтобы вода в нем держалась на постоянном уровне h=8,3 см.
Дано:
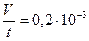 л/с
л/с
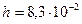 м
м
Найти: 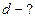
Решение:
Согласно формуле Торричелли: 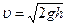 .
.
Учитывая, что 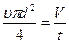 , запишем
, запишем 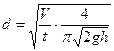 .
.
Находим числовое значение:
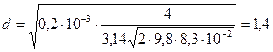 см.
см.
Ответ: 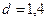 см.
см.
97. При движении шарика радиусом r=3 мм в глицерине ламинарное обтекание наблюдается при скорости шарика, не превышающей 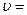 23 см/с. При какой минимальной скорости шара радиусом r=5,5 мм в воде обтекание примет турбулентный характер?
23 см/с. При какой минимальной скорости шара радиусом r=5,5 мм в воде обтекание примет турбулентный характер?
Дано:
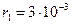 м
м
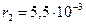 м
м
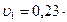 м/с
м/с
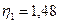 Па·с
Па·с
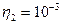 Па·с
Па·с
Найти: 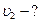
Решение:
Число Рейнольдса для турбулентного потока больше, чем для ламинарного: 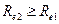 .
.
Тогда 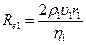 и
и 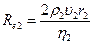 .
.
Коэффициенты динамической вязкости глицерина и воды равны: 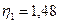 Па·с и
Па·с и 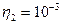 Па·с.
Па·с.
Откуда 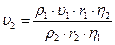 .
.
Находим числовое значение:
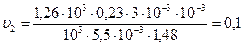 мм/с.
мм/с.
Ответ: 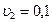 мм/с.
мм/с.
107. Определить относительное удлинение медного стержня, если при его растяжении затрачена работа А=0,12 Дж. Длина стержня l=2 м, площадь поперечного сечения S=1 мм2.
Дано:
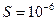 м2
м2
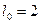 м
м
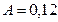 Дж
Дж
Найти: 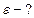
Решение:
Относительное удлинение 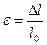 .
.
Работа растяжения  .
.
Тогда 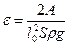 .
.
Находим числовое значение:
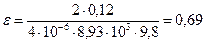 .
.
Ответ: 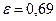 .
.
117. В цилиндре под невесомым поршнем находился воздух в объеме V1=2,4 л при температуре t1=260C и атмосферном давлении p1=730 мм. рт. ст. После погружения цилиндра в воду с температурой t2=120C на глубину h объем воздуха уменьшился до V2=1,9 л. Определить глубину h.
Дано:
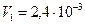 м3
м3
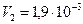 м3
м3
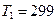 К
К
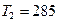 К
К
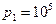 Па
Па
Найти: 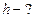
Решение:
Согласно уравнению Менделеева-Клапейрона:
– для первого состояния 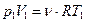 ;
;
– для второго состояния 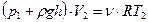 .
.
Тогда 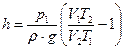 .
.
Находим числовое значение:
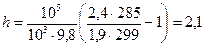 м.
м.
Ответ: 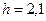 м.
м.
167. Тонкий очень длинный стержень равномерно заряжен с линейной плотностью заряда τ=10 мкКл/м. На перпендикуляре к оси стержня, идущем из его середины, находится точечный заряд 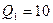 нКл. Расстояние от конца стержня до заряда d=20 см. Определить силу взаимодействия заряженного стержня и точечного заряда.
нКл. Расстояние от конца стержня до заряда d=20 см. Определить силу взаимодействия заряженного стержня и точечного заряда.
Дано:
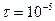 Кл/м
Кл/м
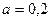 м
м
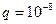 Кл
Кл
Найти: 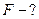
Решение:
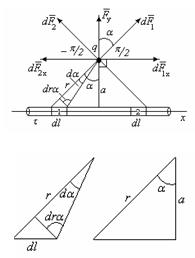
 или
или 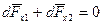 .
.
По закону Кулона сила взаимодействия между q и 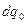 :
: 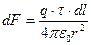 .
.
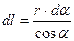 ;
; 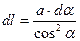 . Откуда
. Откуда 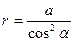 . Тогда
. Тогда 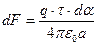 .
.
Проекция на ось Y: 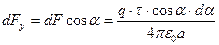 .
.
Откуда 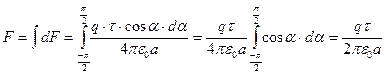 .
.
Находим числовое значение: 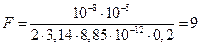 мН.
мН.
Ответ: 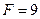 мН.
мН.
187. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского-Гаусса и принцип суперпозиций полей, найти зависимость 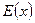 напряженности электрического поля от расстояния для областей: I, II и III. Принять σ1= σ, σ2= -2σ; 2) вычислить напряженность поля в точке, расположенной справа от плоскостей, и указать направление вектора напряженности. Принять σ=20 нКл/м2; 3) построить график
напряженности электрического поля от расстояния для областей: I, II и III. Принять σ1= σ, σ2= -2σ; 2) вычислить напряженность поля в точке, расположенной справа от плоскостей, и указать направление вектора напряженности. Принять σ=20 нКл/м2; 3) построить график 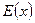 .
.
Дано:
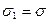
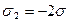
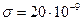 Кл/м2
Кл/м2
Найти: 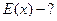
Решение:
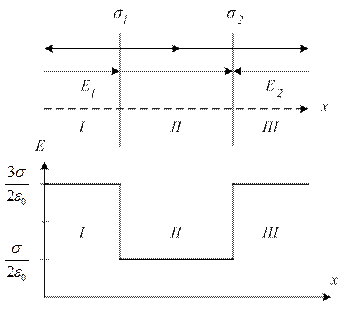
Напряженности однородных электрических полей, создаваемых первой и второй плоскостями, соответственно равны 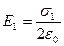 и
и 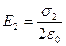 .
.
Напряженности суммарных полей:
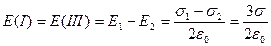 .
.
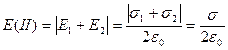 .
.
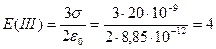 кВ/м.
кВ/м.
Ответ: 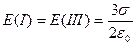 ,
, 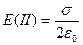 ,
, 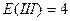 кВ/м.
кВ/м.
197. Тонкий стержень согнут в полукольцо. Стержень заряжен с линейной плотностью τ=133 нКл/м. Какую работу надо совершить, чтобы перенести заряд Q=6,7 нКл из центра полукольца в бесконечность?
Дано:
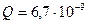 Кл
Кл
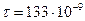 Кл/м
Кл/м
Найти: 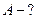
Решение:
Работа сил поля по перемещению заряда 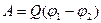 .
.
Электрический потенциал полукольца 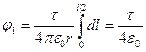 ,
,
где электрическая постоянная 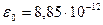 Ф/м.
Ф/м.
Тогда, учитывая, что 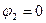 (в бесконечности электрическое поле отсутствует), Запишем итоговое выражение
(в бесконечности электрическое поле отсутствует), Запишем итоговое выражение 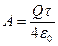 .
.
Находим числовое выражение:
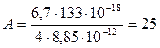 мкДж.
мкДж.
Ответ: 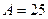 мкДж.
мкДж.
177. По тонкому полукольцу равномерно распределен заряд Q=31,4 нКл с линейной плотностью τ=0,1 мкКл/м. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, совпадающей с центром кривизны полукольца.
Дано:
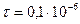 Кл/м
Кл/м
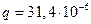 Кл
Кл
Найти: 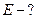
Решение:
Напряженность в точке, совпадающей с центром кольца 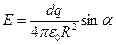 .
.
Тогда 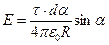 .
.
Интегрируем 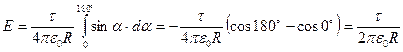 .
.
Тогда 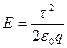 .
.
Находим числовое значение:
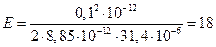 В/м.
В/м.
Ответ: 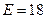 В/м.
В/м.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|