
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вологодский государственный университет»
федеральное государственное бюджетное образовательное учреждение высшего образования
«Вологодский государственный университет»
_Институт машиностроения, энергетики и транспорта
(наименование института)
_______Кафедра электрооборудования____
(наименование кафедры)
КОНТРОЛЬНАЯ РАБОТА
Дисциплина: «__________Физика____________________________»
Наименование темы: «______________________________________»
Шифр работы КР _13.03.02 44.02 03 2020_______________________
код специальности/направления код кафедры регистрационный номер по журналу год
| Руководитель | Мелконян Шушаник Размиковна |
| (уч. степень, звание, должность. Ф.И.О) | |
| Выполнил (а) студент | Бударин Владислав Евгеньевич |
| (Ф.И.О) | |
| Группа, курс | 5б13 ЭО №14/зу |
| Дата сдачи | |
| Дата защиты | |
| Оценка по защите | |
| (подпись преподавателя) |
Вологда
_2020___ г
3. Кабина лифта, у которой расстояние от пола до потолка равно 2,7 м, начала подниматься с постоянным ускорением 1,2 м/с2. Через 2 с после начала подъема с потолка кабины стал падать болт. Найти: а) время свободного падения болта; б) перемещение и путь болта за время свободного падения в системе отсчета, связанной с шахтой лифта.
Дано:
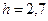 м
м
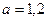 м/с2
м/с2
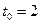 с
с
Найти: 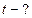 ,
, 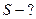 ,
, 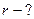
Решение:
Для кабины лифта: 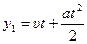 ,
, 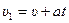 .
.
Для болта: 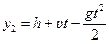 ,
, 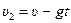 .
.
Когда болт упадет на пол, будет выполняться условие:
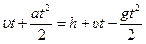 , откуда
, откуда 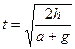 .
.
Тогда 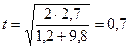 с.
с.
Скорость лифта в момент отрыва болта (относительно шахты):
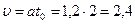 м/с.
м/с.
Перемещение болта 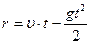 , тогда
, тогда 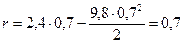 м.
м.
Учитывая, что скорость болта относительно шахты 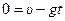 , запишем
, запишем 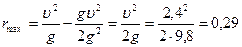 м.
м.
Путь болта 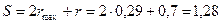 м.
м.
Ответ: 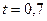 с,
с, 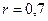 м,
м, 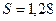 м.
м.
13. На разных склонах наклонной плоскости, образующих с горизонтом углы 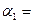 320 и
320 и 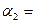 480, находятся грузы m1=3,3 кг и m2. Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и наклонной плоскостью равен 0,1, ускорение грузов а= -1,2 м/с2 (а > 0, если система движется в сторону груза m2). Определить массу второго груза m2.
480, находятся грузы m1=3,3 кг и m2. Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и наклонной плоскостью равен 0,1, ускорение грузов а= -1,2 м/с2 (а > 0, если система движется в сторону груза m2). Определить массу второго груза m2.
Дано:
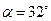
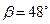
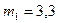 кг
кг
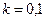
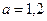 м/с2
м/с2
Найти: 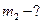
Решение:
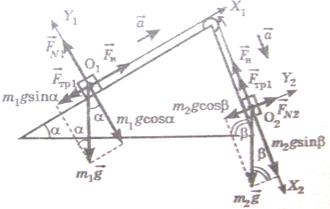
По второму закону Ньютона: 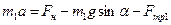 ,
,
где 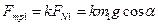 .
.
Аналогично 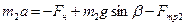 , где
, где 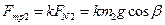 .
.
Тогда 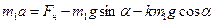 ,
, 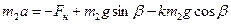 .
.
Откуда 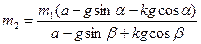 .
.
Находим числовое значение: 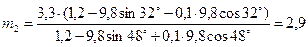 кг.
кг.
Ответ: 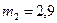 кг.
кг.
23. Снаряд, летящий со скоростью 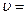 750 м/с, разрывается на два осколка массами m1=45 кг и m2=17 кг, разлетающиеся под углом
750 м/с, разрывается на два осколка массами m1=45 кг и m2=17 кг, разлетающиеся под углом 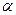 со скоростями u1= 710 м/с и u2=900 м/с. Определить угол
со скоростями u1= 710 м/с и u2=900 м/с. Определить угол 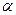 .
.
Дано:
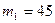 кг
кг
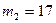 кг
кг
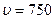 м/с
м/с
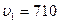 м/с
м/с
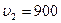 м/с
м/с
Найти: 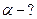
Решение:

Закон сохранения импульса в векторном виде: 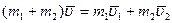 .
.
Воспользуемся теоремой косинусов 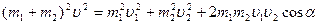 .
.
Тогда 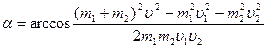 .
.
Находим числовое значение: 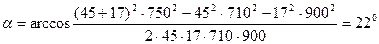 .
.
Ответ: 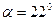 .
.
33. Молот массой m1=5 кг ударяет о небольшой кусок железа, лежащий на наковальне. Масса наковальни m2=100 кг. Массой куска железа пренебречь. Удар неупругий. Определить КПД удара молота при данных условиях.
Дано:
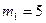 кг
кг
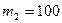 кг
кг
Найти: 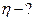
Решение:
Молот до удара обладал энергией 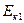 , а
, а 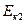 – энергия, переданная фундаменту.
– энергия, переданная фундаменту.
Следовательно, на деформацию использовалась энергия 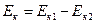 .
.
Коэффициент полезного действия выразим формулой: 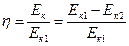 .
.
Найдем взаимосвязь кинетических энергий 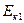 и
и 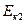 .
.
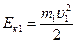 , где
, где 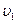 – скорость молота в момент удара.
– скорость молота в момент удара.
Чтобы определить энергию, переданную фундаменту, предварительно найдем скорость системы молот – кусок железа (с наковальней) через закон сохранения импульса: 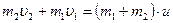 , где
, где 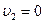 – скорость куска железа с наковальней до удара.
– скорость куска железа с наковальней до удара.
При неупругом ударе деформация не восстанавливается, следовательно, молот с куском железа движутся со скоростью u.
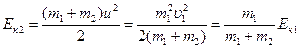 .
.
Тогда найдем коэффициент полезного действия 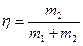 .
.
Находим числовое значение: 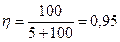 .
.
Ответ: 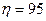 %.
%.
83. В широкой части горизонтально расположенной трубы нефть течет со скоростью 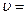 2 м/с. Определить скорость нефти в узкой части трубы, если разность давлений в широкой и узкой частях ее равна
2 м/с. Определить скорость нефти в узкой части трубы, если разность давлений в широкой и узкой частях ее равна 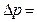 6,65 кПа. Плотность нефти
6,65 кПа. Плотность нефти 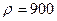 кг/м3.
кг/м3.
Дано:
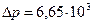 Па
Па
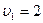 м/с
м/с
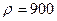 кг/м3
кг/м3
Найти: 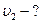
Решение:
Согласно закону Бернулли: 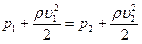 , тогда
, тогда 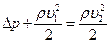 .
.
Откуда 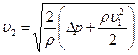 , где плотность нефти
, где плотность нефти 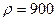 кг/м3.
кг/м3.
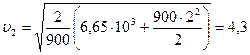 м/с.
м/с.
Ответ: 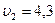 м/с.
м/с.
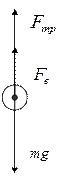
93. Латунный шарик диаметром d=0,5 мм падает в глицерине. Определить: а) скорость установившегося движения шарика; б) является ли при этом значении скорости обтекание шарика ламинарным? Критическое значение числа Рейнольдса Reкр = 0,5.
Дано:
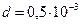 м
м
Найти: 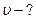 ,
, 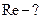
Решение:
По второму закону Ньютона: 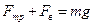 ,
,
где 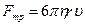
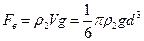
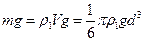
Откуда 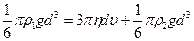 . Скорость
. Скорость 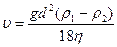 ,
,
где 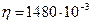 Па·с – динамическая вязкость глицерина;
Па·с – динамическая вязкость глицерина;
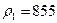 кг/м3 – плотность латуни;
кг/м3 – плотность латуни;
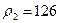 кг/м3 – плотность глицерина.
кг/м3 – плотность глицерина.
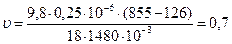 мм/с
мм/с
Число Рейнольдса 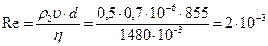 .
.
Ответ: 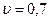 мм/с,
мм/с, 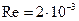 , ламинарное.
, ламинарное.
103. Какую работу нужно совершить, чтобы растянуть на 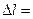 1 мм стальной стержень длиной l=1 м и площадью поперечного сечения S=1 см2?
1 мм стальной стержень длиной l=1 м и площадью поперечного сечения S=1 см2?
Дано:
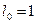 м
м
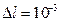 м
м
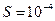 м2
м2
Найти: 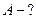
Решение:
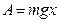 , где модуль перемещения центра масс
, где модуль перемещения центра масс 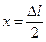 .
.
Тогда 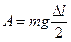 .
.
Учитывая, что 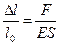 , где
, где 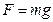 , запишем
, запишем 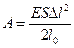 .
.
Модуль Юнга для стали 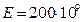 Па.
Па.
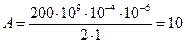 Дж.
Дж.
Ответ: 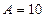 Дж.
Дж.
113. В баллоне объемом V=0,15 м3 находится смесь кислорода и гелия. Число молекул кислорода N1=5,1∙1021, а число молекул гелия N2. Давление смеси р=460 Па, среднее значение молярной массы смеси 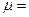 13 кг/кмоль. Определить температуру смеси.
13 кг/кмоль. Определить температуру смеси.
Дано:
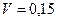 м3
м3
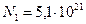
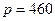 Па
Па
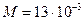 кг/моль
кг/моль
Найти: 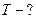
Решение:
Закон Дальтона: 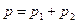 , где
, где 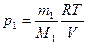 и
и 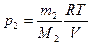 .
.
Тогда 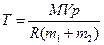 , где
, где 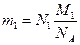 .
.
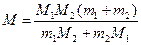 , где
, где 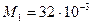 кг/моль и
кг/моль и 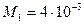 кг/моль.
кг/моль.
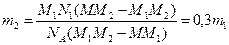 .
.
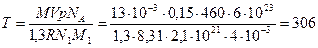 К.
К.
Ответ: 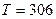 К.
К.
163. Два одинаковых заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол α. Шарики погружают в масло. Какова плотность масла ρ, если угол расхождения нитей при погружении в масло остается тем же? Плотность материала шариков 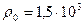 кг/м3, диэлектрическая проницаемость масла ε=2,2.
кг/м3, диэлектрическая проницаемость масла ε=2,2.
Дано:
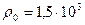 кг/м3
кг/м3
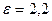
Найти: 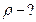
Решение:
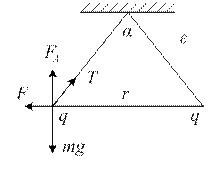
Согласно второму закону Ньютона: 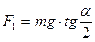 и
и 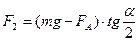 ,
,
где 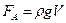 – сила Архимеда.
– сила Архимеда.
По закону Кулона: 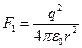 и
и 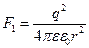 .
.
Тогда 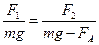 , откуда
, откуда 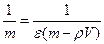 .
.
Учитывая, что 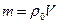 , тогда
, тогда 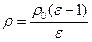 .
.
Находим числовое значение: 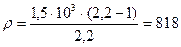 кг/м3.
кг/м3.
Ответ: 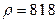 кг/м3.
кг/м3.
173. Определить напряженность поля, создаваемого зарядом, равномерно распределенным по тонкому прямому стержню длиной l=40 см с линейной плотностью τ=200 нКл/м в точке, лежащей на продолжении оси стержня на расстоянии d=20 см от ближайшего конца.
Дано:
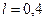 м
м
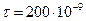 Кл/м
Кл/м
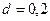 м
м
Найти: 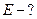
Решение:
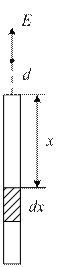
Разобьем на бесконечно малые элементы dx. Каждый элемент на расстоянии d от конца стержня создает поле: 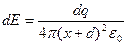 .
.
Учитывая, что 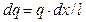 , найдем суммарное поле от всех элементов:
, найдем суммарное поле от всех элементов:
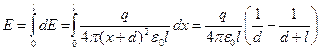 .
.
Учитывая, что 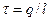 , запишем
, запишем 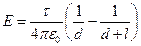 .
.
Находим числовое значение: 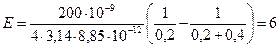 кВ/м.
кВ/м.
Ответ: 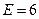 кВ/м.
кВ/м.
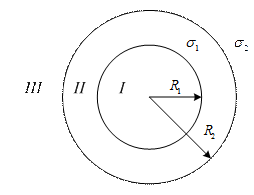
183. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского-Гаусса, найти зависимость 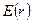 напряженности электрического поля от расстояния для областей: I, II и III. Принять σ1= -4σ, σ2=σ; 2) вычислить напряженность поля в точке, удаленной от центра на расстояние r, и указать направление вектора напряженности. Принять σ=50 нКл/м2, r=1,5R; 3) построить график
напряженности электрического поля от расстояния для областей: I, II и III. Принять σ1= -4σ, σ2=σ; 2) вычислить напряженность поля в точке, удаленной от центра на расстояние r, и указать направление вектора напряженности. Принять σ=50 нКл/м2, r=1,5R; 3) построить график 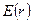 .
.
Дано:
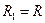
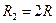
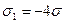
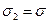
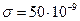 Кл/м2
Кл/м2
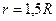
Найти: 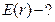 ,
, 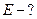
Решение:
Область I: 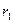 <
< 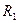
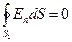 , тогда
, тогда 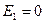
Область II: 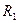 <
< 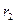 <
< 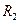
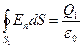 , тогда
, тогда 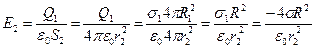 .
.
Область III: 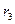 >
> 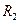
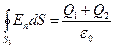 , тогда
, тогда 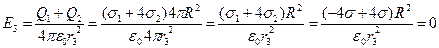 .
.
Находим числовое значение: 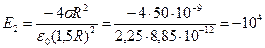 В/м.
В/м.
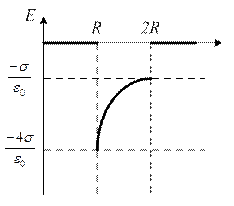
Ответ: 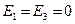 ,
, 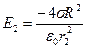 ,
, 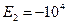 В/м.
В/м.
193. Тонкая нить длиной 60 см заряжена с линейной плотностью 2 нКл/м. Определить потенциал электростатического поля в точке, находящейся на расстоянии 40 см от середины нити и равноудаленной от ее концов.
Дано:
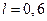 м
м
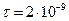 Кл/м
Кл/м
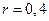 м
м
Найти: 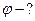
Решение:
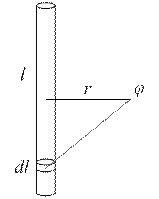
Общая длина нити 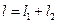 , линейная плотность заряда
, линейная плотность заряда 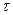 .
.
Используем формулу для расчета потенциала заряженного тела
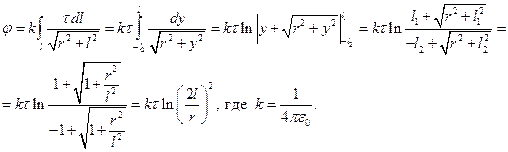
Вычисляем 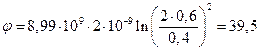 В.
В.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|