
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вологодский государственный университет»
федеральное государственное бюджетное образовательное учреждение высшего образования
«Вологодский государственный университет»
Институт машиностроения, энергетики и транспорта
Кафедра Электрооборудования
КОНТРОЛЬНАЯ РАБОТА
Дисциплина: «Физика »
Наименование темы: «Контрольная работа»
Шифр работы «КР 13.03.02.4402022020»
| Руководитель | Мелконян Шушаник Размиковна |
| (уч. степень, звание, должность. Ф.И.О) | |
| Выполнил (а) студент | Гришкин Николай Юрьевич |
| (Ф.И.О) | |
| Группа, курс | 5Б 13 ЭО-14/ЗУ, 1 курс |
| Дата сдачи | |
| Дата защиты | |
| Оценка по защите | |
| (подпись преподавателя) |
Вологда
2020 г.
2. Две частицы движутся с ускорением g в однородном поле силы тяжести. В начальный момент частицы находились в одной точке и имели скорости 3 м/с и 4 м/с, направленные горизонтально в противоположные стороны. Найти расстояние между частицами в момент, когда векторы их скоростей окажутся взаимно перпендикулярными.
Дано:
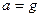
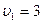 м/с
м/с
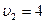 м/с
м/с
Найти:
Решение:
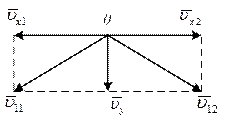
Если 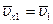 и
и 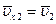 , то
, то 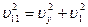 и
и 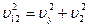 .
.
По теореме Пифагора 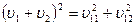 .
.
Тогда 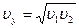 . Учитывая, что
. Учитывая, что 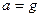 и
и 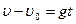 , запишем
, запишем 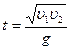 (
( 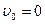 ).
).
Так как поле тяжести однородное, то изменение расстояния вызвано только начальными скоростями, направленными горозонтально.
Тогда 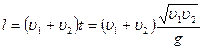 . Вычисляем:
. Вычисляем: 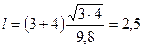 м.
м.
Ответ: 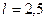 м.
м.
12. На верхнем конце наклонной плоскости укреплен легкий блок, через который перекинута нить с грузами m1=1,7 кг и m2=0,4 кг на концах. Груз m1 скользит вниз по наклонной плоскости, поднимая висящий на другом конце нити груз m2. Угол наклонной плоскости с горизонтом 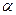 =480, ускорение грузов а=2,1 м/с2. Определить коэффициент трения между грузом m1 и плоскостью.
=480, ускорение грузов а=2,1 м/с2. Определить коэффициент трения между грузом m1 и плоскостью.
Дано:
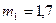 кг
кг
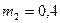 кг
кг
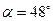
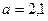 м/с2
м/с2
Найти: 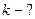
Решение:
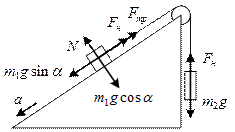
Векторный вид: 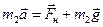
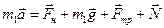
По второму закону Ньютона: 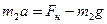 ,
,
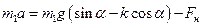 .
.
Откуда 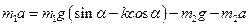 . Тогда
. Тогда 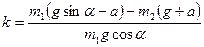 .
.
Находим числовое значение: 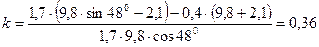 .
.
Ответ: 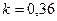 .
.
22. Две лодки массами m1=310 кг и m2=160 кг идут параллельными курсами со скоростями 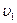 и
и 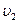 . Когда лодки оказываются рядом, из каждой лодки в другую перекладывается мешок массой m=25 кг, после чего лодки продолжают двигаться параллельными курсами, но со скоростями u1= -1,7 м/с и u2=2,8 м/с. Найти скорость
. Когда лодки оказываются рядом, из каждой лодки в другую перекладывается мешок массой m=25 кг, после чего лодки продолжают двигаться параллельными курсами, но со скоростями u1= -1,7 м/с и u2=2,8 м/с. Найти скорость 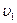 .
.
Дано:
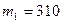 кг
кг
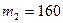 кг
кг
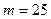 кг
кг
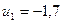 м/с
м/с
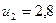 м/с
м/с
Найти: 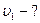
Решение:
По закону сохранения импульса:
– для первой лодки: 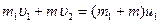 ;
;
– для второй лодки: 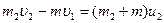 .
.
Тогда 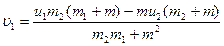 .
.
Находим числовое значение: 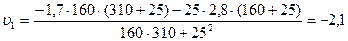 м/с.
м/с.
Ответ: 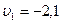 м/с.
м/с.
32. Из пружинного пистолета с жёсткостью пружины k=150 Н/м был произведен выстрел пулей массой m=8 г. Определить скорость пули при выстреле её из пистолета, если пружина была сжата на 4 см.
Дано:
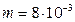 кг
кг
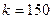 Н/м
Н/м
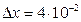 м
м
Найти: 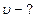
Решение:
Кинетическая энергия пули после выстрела 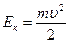 .
.
Энергия деформированной пружины: 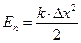 .
.
Согласно закону сохранения энергии 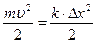 , откуда
, откуда 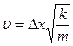 .
.
Вычисляем: 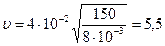 м/с.
м/с.
Ответ: 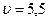 м/с.
м/с.
82. Вода течёт в горизонтально расположенной трубе переменного сечения. Скорость воды в широкой части трубы 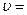 20 см/с. Определить скорость в узкой части трубы, диаметр которой в 1,5 раза меньше диаметра широкой части.
20 см/с. Определить скорость в узкой части трубы, диаметр которой в 1,5 раза меньше диаметра широкой части.
Дано:
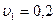 м/с
м/с
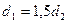
Найти: 
Решение:
Уравнение неразрывности струи 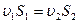 , где площадь
, где площадь 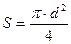 .
.
Откуда 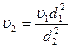 . Находим числовое значение:
. Находим числовое значение: 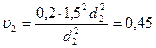 м/с.
м/с.
Ответ: 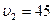 см/с.
см/с.
92. По трубе течет машинное масло. Максимальная скорость, при которой движение масла в этой трубе остается ещё ламинарным, равна 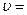 3,2 см/с. При какой скорости движение глицерина в той же трубе переходит из ламинарного в турбулентное?
3,2 см/с. При какой скорости движение глицерина в той же трубе переходит из ламинарного в турбулентное?
Дано:
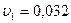 м/с
м/с
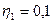 Па·с
Па·с
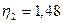 Па·с
Па·с
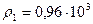 кг/м3
кг/м3
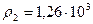 кг/м3
кг/м3
Найти: 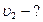
Решение:
Число Рейнольдса для потока жидкости в трубе: 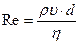 . Тогда
. Тогда 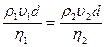 .
.
Откуда 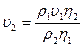 . Подставляем числовые значения:
. Подставляем числовые значения: 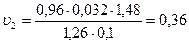 м/с.
м/с.
Ответ: 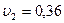 м/с.
м/с.
102. К вертикальной проволоке длиной l=5 м и площадью поперечного сечения S=2 мм2 подвешен груз массой 5,1 кг. В результате проволока удлинилась на 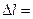 0,6 мм. Найти модуль Юнга материала проволоки.
0,6 мм. Найти модуль Юнга материала проволоки.
Дано:
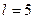 м
м
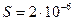 м2
м2
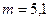 кг
кг
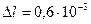 м
м
Найти: 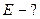
Решение:
Решение:
Согласно закону Гука: 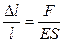 , где сила
, где сила 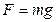 . Тогда
. Тогда 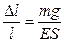 . Откуда
. Откуда 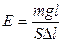 .
.
Находим числовое значение: 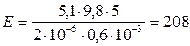 ГПа.
ГПа.
Ответ: 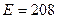 ГПа.
ГПа.
112. В баллоне объёмом V находится смесь кислорода и гелия. Число молекул кислорода N1, а число молекул гелия N2=1,2∙1021. Температура смеси Т=530 К, давление смеси p=250 Па, среднее значение молярной массы смеси 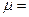 22 кг/кмоль. Определить объём V.
22 кг/кмоль. Определить объём V.
Дано:
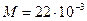 кг/моль
кг/моль
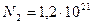
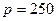 Па
Па
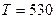 К
К
Найти: 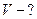
Решение:
Масса газа 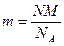 .
.
Аналогично масса кислорода 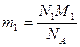 и масса гелия
и масса гелия 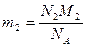 .
.
Уравнение Менделеева-Клапейрона: 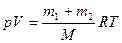 . Тогда
. Тогда 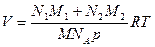 .
.
Найдем число молекул кислорода: 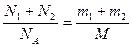 ;
; 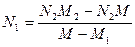 .
.
Находим числовое значение: 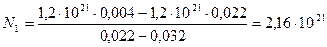 .
.
Тогда 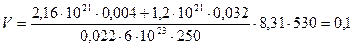 м3.
м3.
Ответ: 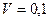 м3.
м3.
162. Два положительных точечных заряда 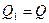 и
и 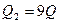 закреплены на расстоянии d=100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.
закреплены на расстоянии d=100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.
Дано:
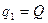
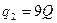
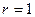 м
м
Найти: 
Решение:
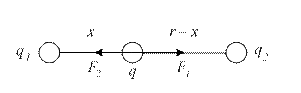
Согласно закону Кулона 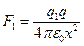 и
и 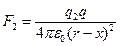 . Откуда
. Откуда 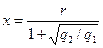 .
.
Находим числовое значение: 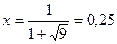 м.
м.
Система зарядов будет находиться в равновесии если 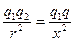 . Тогда
. Тогда 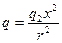 .
.
Находим числовое значение:
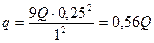 .
.
Ответ: 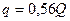 ; в случае положительного заряда равновесие будет устойчивым, отрицательного – неустойчивым; заряд должен находится на расстоянии
; в случае положительного заряда равновесие будет устойчивым, отрицательного – неустойчивым; заряд должен находится на расстоянии 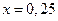 м от заряда
м от заряда 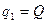 .
.
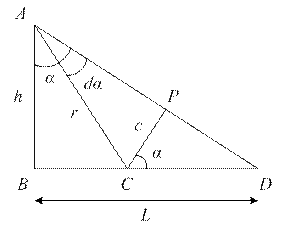
172. Тонкий стержень длиной l=12 см заряжен с линейной плотностью τ=400 нКл/м. Найти напряженность электрического поля в точке, расположенной на перпендикуляре к стержню, проведенному через один из его концов на расстоянии d=8 см.
Дано:
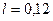 м
м
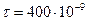 Кл/м
Кл/м
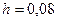 м
м
Найти: 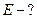
Решение:
Напряженность электрического поля 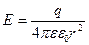 .
.
Учитывая, что 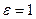 , запишем
, запишем 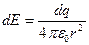 .
.
Линейная плотность 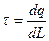 . Откуда
. Откуда 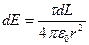 .
.
Из треугольника АВС 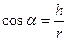 . Из треугольника CHD
. Из треугольника CHD 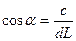 .
.
Из треугольника CAH 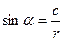 .
.
Тогда 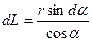
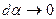
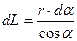 .
.
Откуда 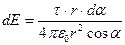
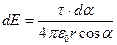
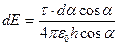
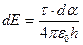 .
.
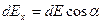 .
.
Из треугольника ABN 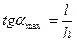 .
.
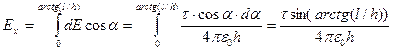 .
.
Находим числовое значение:
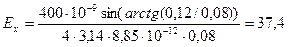 кВ/м.
кВ/м.
Ответ: 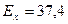 кВ/м.
кВ/м.
182. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского-Гаусса, найти зависимость 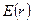 напряженности электрического поля от расстояния для областей: I, II и III. Принять σ1= σ, σ2= -σ; 2) вычислить напряженность поля в точке, удаленной от центра на расстояние r, и указать направление вектора напряженности. Принять σ=0,1 мкКл/м2, r=3R; 3) построить график
напряженности электрического поля от расстояния для областей: I, II и III. Принять σ1= σ, σ2= -σ; 2) вычислить напряженность поля в точке, удаленной от центра на расстояние r, и указать направление вектора напряженности. Принять σ=0,1 мкКл/м2, r=3R; 3) построить график 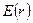 .
.
Дано:
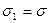
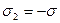
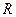 ,
, 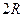
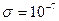 Кл/м2
Кл/м2
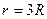
Найти: 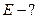 ,
, 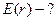
Решение:
Заметим, что точки, в которых требуется найти напряжённость электрического поля, лежат в трёх областях: область I (r1 < R), области II (R < r2 < 2R), области III (r3 > 2R).
1. Для определения напряжённости E1 в области I проведём гауссову поверхность S1 радиусом r1 и воспользуемся теоремой Остроградского-Гаусса: 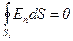 . Из соображений симметрии Еn = E1 = const. Следовательно,
. Из соображений симметрии Еn = E1 = const. Следовательно, 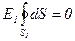 и Е1 (напряжённость поля в области I) во всех точках, удовлетворяющих условию r1 < R, будет равна 0.
и Е1 (напряжённость поля в области I) во всех точках, удовлетворяющих условию r1 < R, будет равна 0.
2. В области II гауссову поверхность проведём радиусом r2. В этом случае (e = 1): 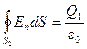 (т.к. внутри гауссовой поверхности находится только заряд Q1).
(т.к. внутри гауссовой поверхности находится только заряд Q1).
Так как En = E = const, то Е можно вынести за знак интеграла: 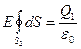 или
или 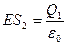 , где
, где 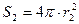 – площадь гауссовой поверхности. Тогда
– площадь гауссовой поверхности. Тогда 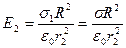 .
.
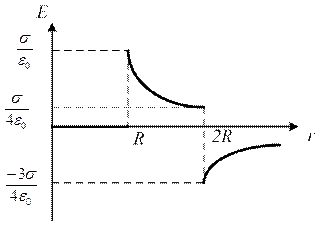 3. В области III гауссова поверхность проводится радиусом r3. Обозначим напряжённость Е области через Е3 и учтём, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен Q1 + Q2. Тогда
3. В области III гауссова поверхность проводится радиусом r3. Обозначим напряжённость Е области через Е3 и учтём, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен Q1 + Q2. Тогда 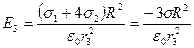 . Откуда
. Откуда 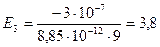 кВ/м.
кВ/м.
Ответ: 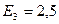 кВ/м.
кВ/м.
192. Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда τ=200 нКл/м. Определить потенциал поля в точке пересечения диагоналей.
Дано:
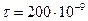 Кл/м
Кл/м
Найти: 
Решение:
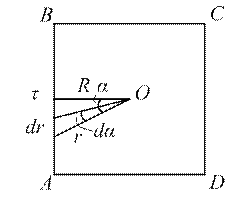
Найдем потенциал от отрезка АВ.
Потенциал в точке О от участка  , который имеет заряд
, который имеет заряд 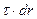 , равен
, равен 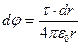 . Из рисунка видно, что
. Из рисунка видно, что 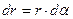 , поэтому
, поэтому 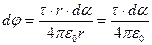 . Тогда полный потенциал от отрезка АВ равен интегралу
. Тогда полный потенциал от отрезка АВ равен интегралу 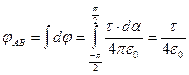 .
.
В виду симметрии задачи потенциал от всей рамки равен 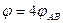 . Тогда
. Тогда 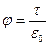 .
.
Находим числовое значение:
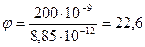 кВ.
кВ.
Ответ: 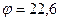 кВ.
кВ.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|