Решение задач.. Задача 1.. Решение.. Задача 2.

№ 9. Решение задач.

Напоминаю формулу:

А ∪ В = А + В - A ∩ B Всего = А + В - АВ

или А + В – АВ = Всего

Иногда сильно путают дополнительные условия. Давайте разберем такие задачи.

Задача 1.

В классе 26 учеников. Из них английский учат 16 человек, немецкий – 13 человек, а 4 человека не желают учить ничего.

Сколько ребят изучают два языка одновременно?

Решение.

Посмотрим, что нам известно.

Кажется, что А ∪ В = 26 Всего – 26

А = 16, В = 13.

Нужно узнать A ∩ B.

Но тут еще мешают 4 бездельника.

Сделаем схему.

Для 4 человек мы нарисовали отдельный круг.

Можем назвать его множеством С. С = 4.

Значит, 26 – это объединение трёх множеств. А ∪ В ∪ С = 26.

Получается, что сначала из общего количества ребят мы должны вычесть количество бездельников. 26 – 4 = 22.

А ∪ В = 22, а не 26.

А дальше знакомо: складываем два кружка, третью цифру вычитаем.

16 + 13 – 22 = 7

A ∩ В = 7.

Задача 2.

В 26 семьях учеников одного класса умеют управлять трактором папы,

в 8 семьях – мамы,

в 3 семьях – и папы, и мамы.

Есть еще 5 семей, в которых трактором управлять не умеет никто.

Сколько всего семей?

Решение:

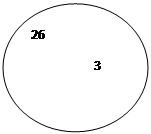Что нам известно здесь? Всего = ?

А = 26, В = 8, A ∩ В = 3.

Да еще имеется 5 семей дополнительно. С = 5.

Нужно узнать всего, то есть А ∪ В ∪ С

Сделаем схему.

Мы видим, что множества А и В пересекаются, при этом три семьи посчитаны дважды.

Значит, нужно найти сначала объединение А ∪ В, а потом уже добавлять к ним множество С.

26 + 8 – 3 = 31. Выходит, что А ∪ В = 31.

Ну а дальше мы должны прибавить к этому числу 5, то есть множество С.

31 + 5 = 36.

А ∪ В ∪ С = 36.