Работа с учебником

Алгебра. Урок №114-115

Тема урока: Применение производной к построению графика функции

Цель урока: Знакомство студентов с общей схемой исследования функций методом построения графика четной и нечетной функции, обучение, проведение, исследование и построение графика.

Ответить на вопросы:

Назовите промежутки:

· убывания

· возрастания,

· экстремумы функции.

Работа с учебником

Самостоятельное изучение нового материала по плану

1 Прочитать текст параграфа «Применение производной к построению графиков функций»

2 Записать в тетрадь схему исследования функции.

Рассмотрим пример:

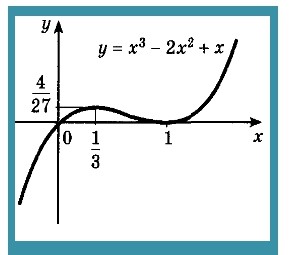
Постройте график функции у= (х) = х³ - 2х² + х.

Решение.

1. Область определения D(f) = R.

2. Найдем производную f'(x) = (х³ - 2х² + х )' = Зх²- 4х +1.

3. Найдем критические точки, решив уравнение f'(x) = 0. Зх²- 4х + 1 = 0,

(Зх-1) (х-1) = 0

Х₁ =1, X₂= 1/3

4. Найдем промежутки возрастания и убывания, используя метод интервалов и правило чередования знаков.

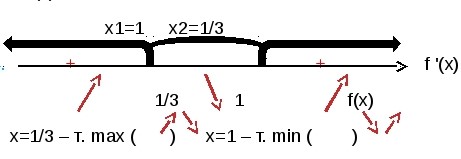
Функция возрастает на промежутках: (-∞, 1/3) и (1,+ ∞), так как f'(x)

Так как f'(x)<0 на промежутке (1/3, 1), значит, функция убывает на этом промежутке.

5. При переходе через точку х = - знак производной меняется с «+» на «-», значит, это точка максимума. При переходе через точку х = 1 знак производной меняется с «-» на «+», значит, это точка минимума. Значения в экстремумах равны:

f (1/3)= (1/3)³-2 (1/3)²+ 1/3= 4/27;

f (1)= 1-2 +1=0

Составим таблицу по результатам исследования

х	(-∞, 1/3)	1/3	(1/3, 1),	(1,+ ∞),
f'(x)	+		-	+
f(х)	↑	4/27		↓

7. Найдем абсциссы точек пересечения графика с осью Ох:
х³ -2х² + х = 0,

Х (х² -2х + 1) =0,

Х (х -1)² =0,

х = 0 или х = 1.

8. Построим график функции.

Выполнить: Построить график функции

а) f(х) = 1- х² -х⁵.

b)у = 6х⁴-4х⁶;

Домашнее задание: Алгебра 10-11 класс Ш. А. Алимов г. Москва Просвещение 2016

&51. Построить графики функции:

а) у = 2+ 5х³ -Зх⁵;

б) у = 4х⁵ -5х⁴;

Отправлять личным сообщением: на станицу https://vk.com/id499100240