Контакты

Случайная статья

апреля 2020 г. (вторник)

14 апреля 2020 г. (вторник)

Дисциплина: Математика

Группа: № 74

Урок № 94-95

Тема: Правила дифференцирования.

Цель: закрепить изученные правила дифференцирования через решение упражнений.

Литература: Алгебра и начала математического анализа. 10-11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни / Ш.А. Алимов, Ю.М. Колягин [и др.] – М.: Просвещение, 2012.

Материалы урока:

Правила дифференцирования

1) (u + v)¢ = u¢ + v¢

2) (u × v)¢ = u¢×v + u×v¢

3) =

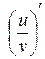Для сложной функции y = f (u), u = u(x)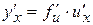

1. Найдите производную функции:

1) f (х) = х² + х³;

f ¢(х) = (х² + х³) ¢ = (х² ) ¢+ (х³) ¢ = 2х + 3х²;

2) f (х) = х² + 3х – 1;

f ¢(х) = (х² + 3х – 1) ¢ = (х² ) ¢+ (3х – 1) ¢ = 2х + 3;

3) f (х) = 4х³ + 2х⁴ – х⁵;

f ¢(х) = (4х³ + 2х⁴ – х⁵) ¢ = (4х³ ) ¢+ (2х⁴) ¢ – (х⁵) ¢ = 4×3х² + 2×4х³– 5х⁴ = 12х² + 8х³– 5х⁴;

4) f (х) = 3х³ + 4х⁵;

f ¢(х) = (3х³ + 4х⁵) ¢ = (3х³) ¢+ (4х⁵) ¢ = 3×3х² + 4×5х⁴ = 9х² + 20х⁴;

5) f (х) = 2х⁸ – 3х⁴ – х + 5;

f ¢(х) = (2х⁸ – 3х⁴ – х + 5) ¢ = (2х⁸) ¢– (3х⁴) ¢ + (– х + 5) ¢ = 2×8х⁷ – 3×4х³– 1 = 16х⁷ – 12х³– 1;

6) ;

;

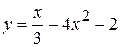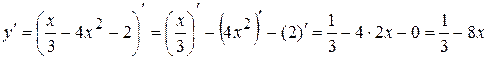7) f (х) = (2х – 3)(1 – х³);

f ¢(х) = ((2х – 3)(1 – х³)) ¢ = (2х – 3) ¢× (1 – х³) + (2х – 3) × (1 – х³)¢ =

= 2(1 – х³) + (2х – 3) × ( – 3х²) = 2 – 2х³– 6х³+ 9х² = – 8х³+ 9х² + 2;

8) ;

;

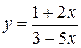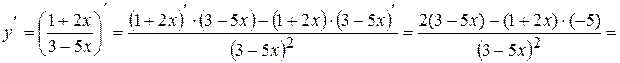
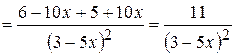9) ;

;

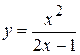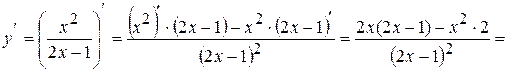
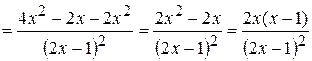10) ;

;

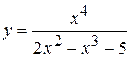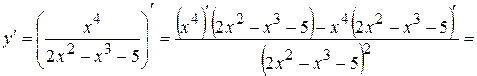
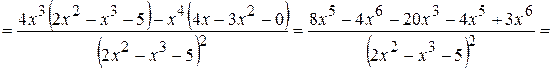
11) ;

.

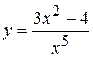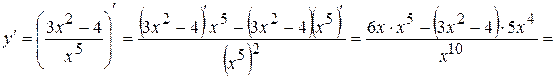
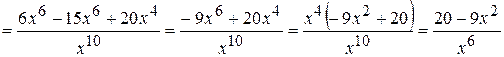2. Найдите h¢(– 4), если .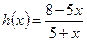

.

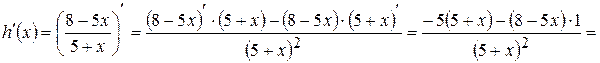
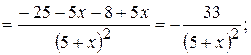
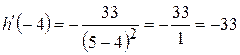3. Найдите f ¢(2) и f ¢(0) , если f (х) = х² – 3х.

f ¢(х) = (х² – 3х) ¢ = (х²) ¢– (3х) ¢ = 2х – 3;

f ¢(2) = 2×2 – 3 = 4 – 3 = 1; f ¢(0) = 2×0 – 3 = 0 – 3 = – 3.

Домашнее задание: выполнить № 806; стр. 243 .

ФОТОГРАФИРУЕМ И ОТСЫЛАЕМ ЕЛЕНЕ АНАТОЛЬЕВНЕ

ВСЕ ВЫПОЛНЕННЫЕ ДОМАШНИЕ ЗАДАНИЯ И КОНТРОЛЬНЫЕ РАБОТЫ!!!!!!!!!!!!!!!!

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.