Хелпикс

Главная

Контакты

Случайная статья



Практическая работа. Закон Мальтуса»



Практическая работа

«Закон Мальтуса»

 

Чаще всего электронные таблицы используются в задачах для получения расчетных ведомостей, смет, справок, списков, т. е. в области делопроизводства. Однако электронные таблицы могут оказаться полезными и для научных целей. С их помощью можно строить компьютерные математические модели, проводить вычислительные эксперименты. Рассмотрим пример такого вычислительного эксперимента.

Ученые установили, что прирост какого-либо вида живых организмов за счет рождаемости прямо пропорционален их количеству, а убыль за счет смертности прямо пропорциональна квадрату их количества. Этот закон известен под названием закона Мальтуса.

Пусть в одном хозяйстве собираются разводить карпов. Прежде чем запускать мальков в пруд, решили провести расчеты. Согласно закону Мальтуса, изменение числа рыб за один год вычисляется по формуле

DN = kN – qN2

Здесь N — число карпов в начале года, k — коэффициент прироста, q — коэффициент смертности. Экспериментально установлено, что для данного вида рыб (карпы) и в данных условиях (состояние водоема, наличие корма) k = 1, q = 0,001.

Если первоначально в пруд запущено N0 рыб, то из закона следует, что количество карпов через год будет таким:

N1 = N0 + (kN0 – qN02)

Через два года:

N2 = N1 + (kN1 – qN12)

и так далее. Можно написать общую формулу для вычисления количества рыб в 1-м году после их запуска:

Ni = Ni-1 + (kNi-1 – qNi-12), i = 1, 2, 3…

Эта формула является математической моделью процесса размножения рыб в водоеме.

Заполним электронную таблицу для проведения по этой формуле расчета рыбного «поголовья» в пруду в течение нескольких лет:

  A B C D E F
k = q = 0,001 N =  
           
Год   Число рыб      
           
  =F1+$B$1*F1-$D$1*F1*F1      
=А5+1   =C5+$B$1*C5-$D$1*C5*C5      
=А6+1   =C6+$B$1*C6-$D$1*C6*C6      
=А7+1   =C7+$B$1*C7-$D$1*C7*C7      
=А8+1   =C8+$B$1*C8-$D$1*C8*C8      
… …   … … … …

Не надо думать, что всю таблицу приходится вводить посимвольно с клавиатуры. Строки, начиная с 7-й, формируются путем копирования предыдущей строки. При этом относительные адреса изменяются автоматически.

Для получения результатов достаточно занести в ячейку F1 первоначальное число рыб.

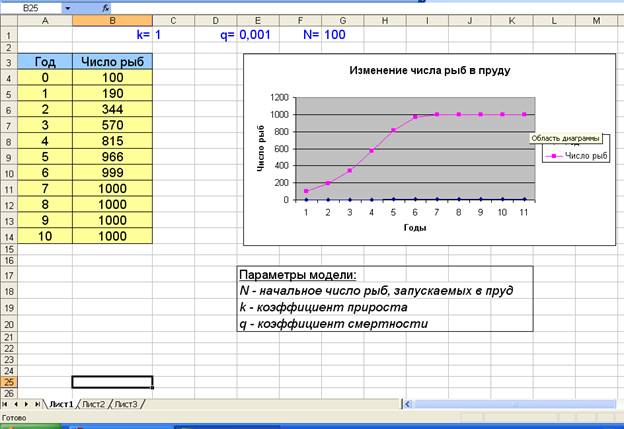
Теперь можно экспериментировать. Проследим, как за 10 лет будет меняться число карпов при разном количестве первоначально запущенных рыб. Вот несколько таблиц с результатами таких расчетов:

 

k = 1 q = 0,001 N = 100  
Год Число рыб
   

 
k = 1 q = 0,001 N = 1500  
Год Число рыб
   

 
k =1 q =0,001 N =2000  
Год Число рыб
   

 

 

Из таблиц следует, что невозможно иметь в пруду 2000 карпов и более. Если начальное число рыб меньше 1000, то оно постепенно будет расти до 1000 штук и далее не будет меняться. Если сразу запустить 1000 рыб, то это количество останется неизменным и в последующие годы. Даже если запустить сначала 1500 рыб, то через год их численность в два раза сократится, а затем все равно дойдет до 1000. Если же запустить в пруд 2000 рыб, то через год все они вымрут.

Из полученных результатов рыбоводы могут сделать практические выводы. Приведенные выше таблицы автоматически получались после изменений значения всего лишь в одной ячейке

 

Проведите вычислительный эксперимент в таблице расчета количества рыб в пруду, поставив следующую цель: подобрать такие значения параметров k и q, при которых количество рыб за 10 лет может быть доведено до 2000. Проведите вычислительный эксперимент в таблице расчета количества рыб в пруду, поставив следующую цель: какое количество рыб должно первоначально быть в пруду, чтобы процесс разведения рыб был экономически выгодным.
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.