Применение производной для отыскания точек экстремума

Применение производной для отыскания точек экстремума

Задание #1

Вопрос: Выберите верные утверждения: После исследования на экстремумы функции 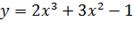получилось, что:

Выберите несколько из 5 вариантов ответа:

1) точка x = 0 - точка максимума 2) точка x = -1 - точка минимума

3) точка x = 0 - точка минимума 4) точка x = -1 - точка максимума

5) функция не имеет экстремумов

Задание #2

Вопрос: Сколько точек минимума имеет функция, изображенная на рисунке?

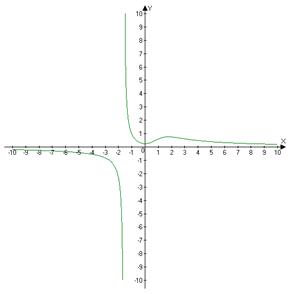Изображение:

Запишите число: ___________________________

Задание #3

Вопрос: Выберите верные условные схемы:

Выберите несколько из 5 вариантов ответа:

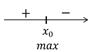1) 2) 3) 4) 5)

Задание #4

Вопрос: Сколько точек максимума имеет функция, изображенная на рисунке?

Изображение: смотри Задание #2

Запишите число: ___________________________

Задание #5

Вопрос: Сколько точек экстремума имеет функция, изображенная на рисунке?

Изображение: смотри Задание #2

Запишите число: ___________________________

Задание #6

Вопрос: Используя данные таблицы, укажите точки экстремума функции f(x):

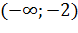
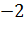
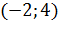
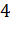
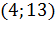
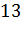
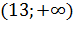
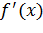
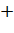
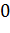
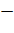
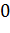
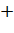
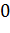
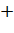
Выберите несколько из 3 вариантов ответа: 1) 4 2) -2 3) 13

Задание #7

Вопрос: Выберите верное утверждение: Функция y = cos x + 2x

Выберите один из 3 вариантов ответа:

1) имеет точки минимума 2) не имеет экстремумов 3) имеет точки максимума

Задание #8

Вопрос: Сколько точек экстремума имеет функция, изображенная на рисунке?

Изображение:

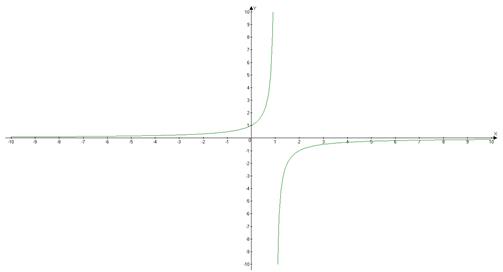
Запишите число: ___________________________

Задание #9

Вопрос: Используя данные таблицы, укажите точку минимума функции f(x):

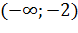
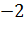
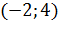
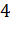
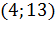
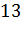
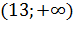
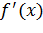
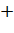
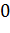
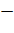
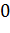
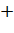
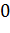
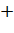
Выберите один из 3 вариантов ответа: 1) -2 2) 13 3) 4

Задание #10

Вопрос: Используя данные таблицы, укажите точку максимума функции f(x):

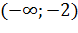
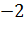
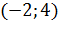
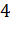
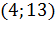
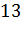
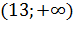
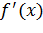
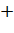
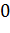
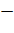
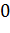
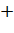
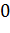
Выберите один из 3 вариантов ответа: 1) 4 2) 13 3) -2