до 13.00 прислатьна почту ответы заданий, выделенных красным(все), по форме: в-1, 1.2 А)… ( выбранная буква и ответ, краткое решение с чертежом задач второй части, дано не писать, объяснения краткие) Раньше указанного срока не присылайте.. Пример 1.. Реш

5.05-7.05 Тема: координаты на плоскости. Ответы для сверки алгебры в конце

Повторяем тему «координаты на плоскости». Все задания из

сборника ГИА в таблице

7.05 до 13.00 прислатьна почту ответы заданий, выделенных красным(все), по форме: в-1, 1.2 А)… ( выбранная буква и ответ, краткое решение с чертежом задач второй части, дано не писать, объяснения краткие) Раньше указанного срока не присылайте.

вариант
№задания					2.3
вариант
№задания	1.5	2.4	2.4	2.4
вариант
№задания		2.4	2.4

Формула вычисления координат середины отрезка с концами A(x₁, y₁) и B(x₂, y₂)

x =	х₁ + x₂		y =	у₁ + y₂

Формула вычисления расстояния между двумя точками A(x₁, y₁) и B(x₂, y₂) на плоскости:

AB = √(x₂ – x₁)² + (y₂ – y₁)²

Пример 1.

Найти координаты точки С, середины отрезка AB заданного точками A(-1; 3) и B(6; 5).

Решение.

x =	х₁ + x₂	=	-1 + 6	=		= 2,5

y =	у₁ + y₂	=	3 + 5	=		= 4

Ответ: С(2,5;4).

Пример 2

Найдите длину медианы АМ в треугольнике АВС, если известны координаты его вершин .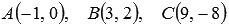

Решение.

Так как АМ – медиана, то точка М является серединой стороны ВС. Найдем координаты середины этого отрезка по известным координатам его концов:

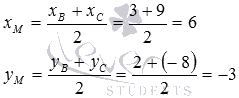
Таким образом, .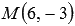

Осталось воспользоваться формулой для вычисления расстояния между точками А и М:

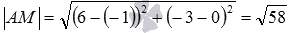
Пример 3 Найти расстояние между точками A(0, 1) и B(2,-2).

Решение.

AB = √(x₂ – x₁)² + (y₂ – y₁)² = √(2 - 0)² + (-2 - 1)² = √2² + (-3)² = √13

Ответ: AB = √13.

Пример 4.На оси ординат найдите точку, равноудаленную от точек А (-3; 5) и В (6; 4).

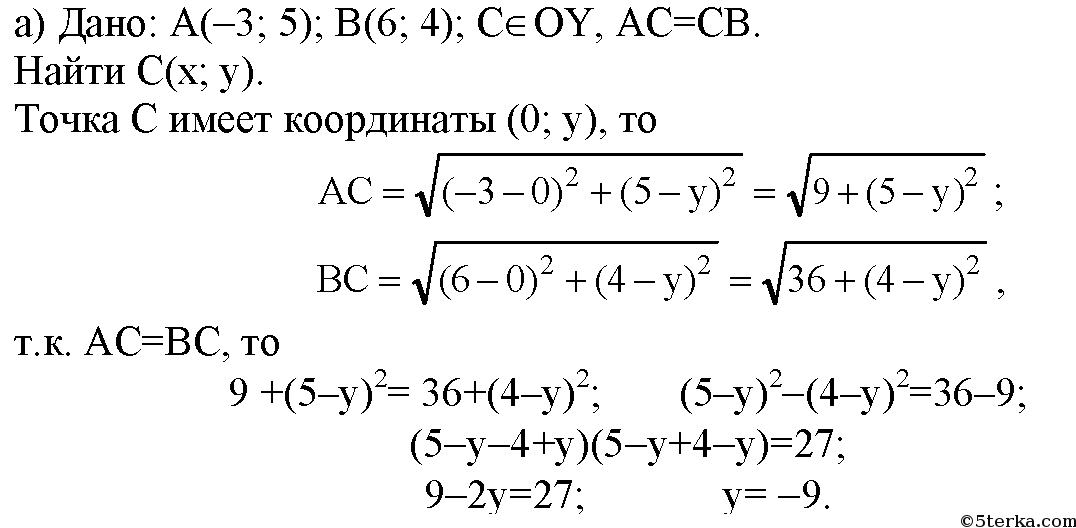
Сверьте свои ответы по теме «неравенства и системы неравенств»

12 Следующая ⇒