
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Закрепление нового материала
Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:
Пример. Решить уравнение: 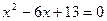 .
.
Решение. Найдем дискриминант: 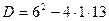 = 36 – 52 = -16.
= 36 – 52 = -16.
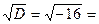
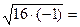
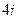 .
.
Тогда 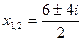
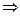
 .
.
Ответ: 
Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.
Подобное утверждение, известное под названием "основная теорема алгебры", было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение п-й степени имеет п комплексных корней (при этом некоторые корни являются кратными). Эти результаты подчеркивают ту исключительную роль, которую играют комплексные числа в теории алгебраических уравнений.
Так вот, в множестве комплексных чисел корень из -1 извлекается и очень хорошо! Вспомним знакомую нам формулу . Корень из -1= i,
Исследование алгебраических уравнений является одним из важнейших вопросов в математике. Например, действительных корней не имеет квадратное уравнение с отрицательным дискриминантом. Простейшим таким уравнением является уравнение
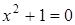 .
.
Для того чтобы это уравнение имело решение, необходимо расширить множество действительных чисел путем присоединения к нему корня уравнения
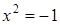 .
.
Обозначим этот корень через 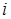 . Таким образом, по определению
. Таким образом, по определению
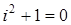 , или
, или
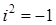 ,
,
следовательно,
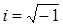 .
.
Таким образом, действительных чисел явно недостаточно, чтобы построить такую теорию квадратных уравнений, в рамках которой каждое квадратное уравнение было бы разрешимо. Это приводит к необходимости расширять множество действительных чисел до множества, в котором было бы разрешимо любое квадратное уравнение. Такое множество называется множеством комплексных чисел и обозначается С.
Рассматривать будем на таком примере:
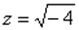
Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:
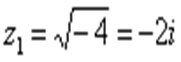
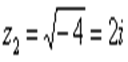
Выполним проверку того, что эти корни и права оказываются решением уравнения:
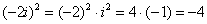
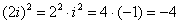
Что и требовалось доказать.
Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: 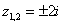 .
.
Такие корни являются сопряженными комплексными корнями.
Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:
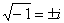 ,
, 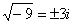 ,
,
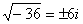 ,
,
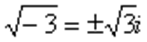 ,
,
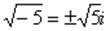
Решим квадратное уравнение 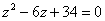 .
.
Первым шагом определим дискриминант уравнения:
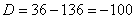
В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:
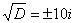
Как известно из формул дискриминанта у нас образуется 2 корня:
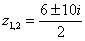
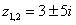 – сопряженные комплексные корни
– сопряженные комплексные корни
Т.о., у уравнения 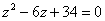 есть 2 сопряженных комплексных корня:
есть 2 сопряженных комплексных корня:
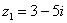 ,
,
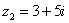
Найти корни квадратного уравнения
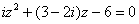
Решение: на первом месте расположена мнимая единица, и, в принципе, от неё можно избавиться (умножая обе части на 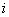 ), однако, в этом нет особой надобности.
), однако, в этом нет особой надобности.
Для удобства выпишем коэффициенты:
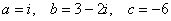
Не теряем «минус» у свободного члена. Уравнение в стандартном виде 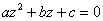 :
:
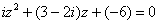
Вычислим дискриминант:
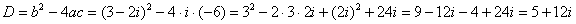
А вот и главное препятствие:
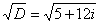
Применение общей формулы извлечения корня осложняется серьёзными затруднениями, связанными с аргументом подкоренного комплексного числа (убедитесь сами). Но существует и другой, «алгебраический» путь! Корень будем искать в виде:

Возведём обе части в квадрат:
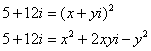
Два комплексных числа равны, если равны их действительные и их мнимые части. Таким образом, получаем следующую систему:
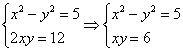
Систему проще решить подбором (более основательный путь – выразить из 2-го уравнения 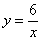 – подставить в 1-е, получить и решить биквадратное уравнение). Из 1-го уравнения следуют, что «икс» по модулю больше, чем «игрек». Кроме того, положительное произведение
– подставить в 1-е, получить и решить биквадратное уравнение). Из 1-го уравнения следуют, что «икс» по модулю больше, чем «игрек». Кроме того, положительное произведение 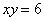 сообщает нам, что неизвестные одного знака. Исходя из вышесказанного, и ориентируясь на 2-е уравнение, запишем все подходящие ему пары:
сообщает нам, что неизвестные одного знака. Исходя из вышесказанного, и ориентируясь на 2-е уравнение, запишем все подходящие ему пары:
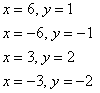
Очевидно, что 1-му уравнению системы удовлетворяют две последние пары, таким образом:
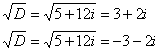
Не помешает промежуточная проверка:
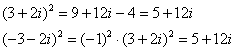
что и требовалось проверить.
В качестве «рабочего» корня можно выбрать любое значение. Понятно, что лучше взять версию без «минусов»: 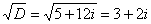
Находим корни, не забывая, кстати, что 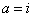 :
:

Ответ: 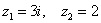
Проверим, удовлетворяют ли найденные корни уравнению 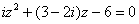 :
:
1) Подставим 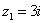 :
:
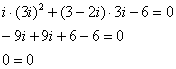
верное равенство.
2)Подставим
 :
:
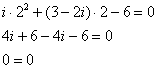
верное равенство.
Таким образом, решение найдено правильно.
4. Закрепление нового материала
Решить уравнения:
1. х2 + (5 – 2i) x + 5(1– i) = 0;
2. х2 + (1 – 2i) х – 2i = 0;
3. 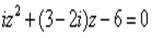
5. Домашнее задание
1. Составить конспект на тему «Тригонометрическая форма записи комплексного числа»;
2. Решить уравнения:
z^2-2z+5=0
z^2+3z+6=0
z^2-4z+25=0
3z^2-3z+3=0
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|