Задача 1.. Задача 3.. Задача 4.

Задача 1.

Окружность составляет ⁰ , поэтому дуга АС, которая составляет части окружности, равняется . Поэтому вписанный угол АВС равен , так как градусная мера вписанного угла вдвое меньше градусной меры дуги, на которую опирается.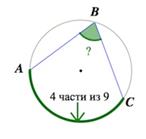

Ответ:

Задача 2.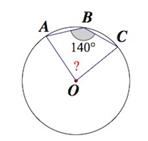

Заметим, тот угол АОС, что помечен на картинке, хоть и является центральным углом, но не является соответствующим для вписанного угла АВС, так как они опираются на разные дуги (угол АВС опирается на дугу АС, а угол АОС — на дугуАВС).

Так как вписанный угол АВС, равный , опирается на дугу АС, то она равна . Значит дуга АВС равна . А значит центральный угол АОС, который измеряется градусной мерой дуги, на которую опирается, равен

Ответ:

Задача 3.

Так как углы ВСА и ВDA опираются на одну дугу (АВ), то они равны, то есть .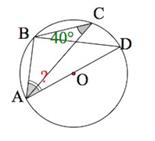

Теперь обратимся к треугольнику АВD. Он прямоугольный, так как угол АВD, опирающийся на диаметр, — прямой. Значит, .

Ответ:

Задача 4.

Найти градусную меру угла, изображенного на рисунке:

Правильный восьмиугольник делит дугу окружности своими вершинами на восемь одинаковых частей, а значит на каждую такую часть приходится

Ответ:

Задача 6.

Задача 5. Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности?

⇐ Предыдущая 12