Задача 13 (демонстрационный вариант 2020 г.).

Стр 1 из 2Следующая ⇒

Задача 13 (демонстрационный вариант 2020 г.).

а) Решите уравнение

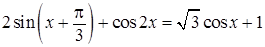б) Укажите корни этого уравнения, принадлежащие отрезку .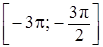

Решение.

а) Запишем исходное уравнение в виде:

; ; .

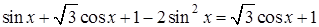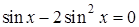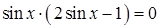Значит, 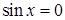, откуда 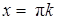, , 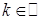или 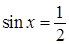, откуда 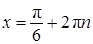, , 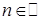или , .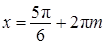

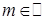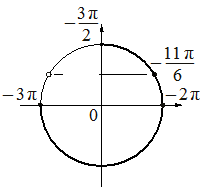
б) С помощью числовой окружности отберём корни, принадлежащие отрезку .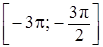

Получим числа: ; ; .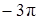

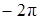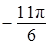Ответ: а) , ; , ;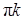

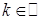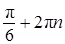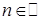Ответ: , ;

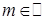Ответ: б) ; ; .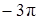

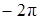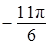Комментарий.

Множество корней может записано по-другому.

Отбор корней может быть произведен любым другим способом: с помощью графика, решения двойных неравенств и т.п.

При отборе корней с помощью числовой (тригонометрической) окружности на числовой окружности должно быть: отмечены и обозначены концы числового отрезка, выделена дуга, отмечены и обозначены корни, принадлежащие данному отрезку. На окружности могут быть отмечены вспомогательные числа, принадлежащие числовому отрезку.

Пример 1.

а) Решите уравнение .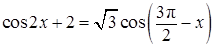

б) Укажите корни этого уравнения, принадлежащие отрезку .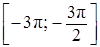

Ответ: а) 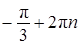, 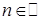; 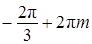, 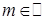; б) ; .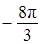

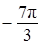Комментарий.

Обоснованно получены верные ответы в обоих пунктах.

Оценка эксперта: 2 балла.

Пример 2.

а) Решите уравнение .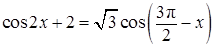

б) Укажите корни этого уравнения, принадлежащие отрезку .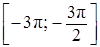

Ответ: а) 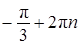, 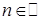; 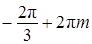, 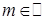; б) ; .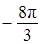

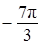Комментарий.

Обоснованно получен верный ответ в пункте а, но отбор корней нельзя назвать обоснованным, так как перебор остановлен на корне, принадлежащем отрезку. Типичный пример выставления 1 балла.

12 Следующая ⇒