ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 52. Краткие теоретические сведения. Образец выполнения заданий. Задача 1.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 52

Тема: Решение задач на пирамиду

Краткие теоретические сведения

Площадь поверхности пирамиды. Полная поверхность пирамиды состоит из поверхности боковой, то есть площади всех боковых граней, и площади основания:

S_полн = S_бок + S_осн

Теорема. Объем пирамиды равен одной трети произведения площади основания на высоту.

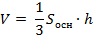
Теорема (о 3^х перпендикулярах). Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и самой наклонной.

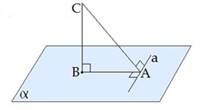
Теорема Пифагора:В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов

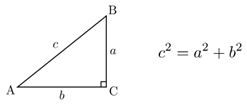
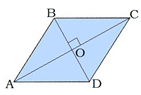
Свойства ромба:

1°. Диагонали ромба точкой пересечения делятся пополам: BO=OD; AO=OC.

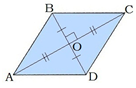
2°. Диагонали ромба взаимно перпендикулярны: AC⊥BD.

Образец выполнения заданий

Задача 1.

Основанием пирамиды является прямоугольник со сторонами 3 и 4 см. Ее объем равен 16 см³. Найдите высоту этой пирамиды.

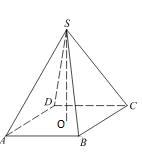
Дано: SABCD – пирамида

ABCD – прямоугольник

AB = 3 см

BC = 4 см

V = 16 см³

Найти: SO = h

Решение:

1. Объем пирамиды вычисляется по следующей формуле:

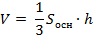
2. Так как в основании прямоугольник, то площадь основания равна

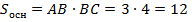(см²)

3. Зная площадь основания и объем, составим и решим уравнение

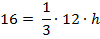
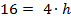
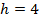(см)

Ответ: 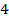см

Задача 2. Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из его диагоналей равна 8 см. Найдите боковые ребра пирамиды, если высота ее проходит через точку пересечения диагоналей основания и равна 3 см.

Дано: KABCD – пирамида

ABCD – ромб

AB = 5 см

AC = 8 см

AC ∩ BD = O

KO = h = 3 см

Найти: KA, KB, KC, KD

Решение:

1. Используя свойство 1° ромба получаем, что AO = OC = 8:2 = 4 см

2. Из свойства 2° ромба получаем, что ∆AOB, ∆BOC, ∆COD, ∆DOA – прямоугольные.

3. Рассмотрим ∆AOB и используем теорему Пифагора, чтобы найти сторону OB:

OB² = AB² – AO²=5² – 4² = 25 – 16 = 9

OB = 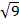= 3 (cм)

4. Найдем KA из ∆KOA – прямоугольного, по теореме Пифагора:

KA² = KO² + AO² = 3² + 4² = 9 + 16 = 25

KA = 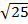= 5 (см)

KA = KC = 5 (см)

5. Найдем KB из ∆KOB – прямоугольного, по теореме Пифагора:

KB² = KO² + BO² = 3² + 3² = 9 + 9 = 18

KB = 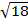= 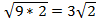(см)

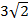KB = KD = (см)

Ответ: KA = KC = 5 см, KB = KD = 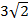см.

Задача 3.Основанием пирамидыDABC является прямоугольный треугольник ABC, у которого гипотенуза AB равна 29 см, а катет AC равен 21 см. Боковое ребро DA перпендикулярно к плоскости основания и равно 20 см. Найдите площадь боковой поверхности пирамиды.

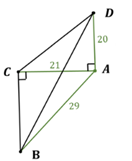
Дано: DABC – пирамида

∆ABC - прямоугольный

AB = 29 см

AC = 21 см

DA 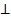(ABC)

DA = 20 см

Найти: S_бок

Решение:

1. По теореме о 3^х перпендикулярах имеем три прямоугольных треугольника: ∆ABD, ∆ACD, ∆BCD

2. Площадь боковой поверхности равна сумме всех ее площадей боковых граней

S_бок=S_∆_ABD + S_∆_ACD + S_∆_BCD

3. S_∆_ABD = 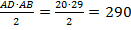(см²)

4. S_∆_ACD= 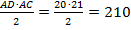(см²)

5. Из ∆ACD по теореме Пифагора выразим CD:

CD² = AC² + DA² = 21²+ 20²= 441 + 400 = 841 = 29²

CD = 29 (cм)

6. Из ∆ABC по теореме Пифагора выразим BC:

BC² = BA^{2 -}AC² = 29²- 21²= 841 - 441 = 400 = 20²

BC = 20 (cм)

7. S_∆BCD = 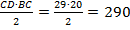(см²)

8. S_бок= 290 + 290 + 210 = 790 (см²)

Ответ: 790 см²

Содержание работы

Вариант 1.

Задание 1.Основанием пирамиды является ромб, сторона которого равна 13 см, а одна из его диагоналей равна 24 см. Найдите боковые ребра пирамиды, если высота ее проходит через точку пересечения диагоналей основания и равна 12 см.

Задание 2.Основанием пирамидыDABC является прямоугольный треугольник ABC, у которого гипотенуза AB равна 17 см, а катет AC равен 15 см. Боковое ребро DA перпендикулярно к плоскости основания и равно 8 см. Найдите площадь боковой поверхности пирамиды.

Задание 3.Основанием пирамиды является прямоугольник со сторонами 5 и 6 см. Ее объем равен

20 см³. Найдите высоту этой пирамиды.

Вариант 2.

Задание 1.Основанием пирамиды является ромб, сторона которого равна 17 см, а одна из его диагоналей равна 30 см. Найдите боковые ребра пирамиды, если высота ее проходит через точку пересечения диагоналей основания и равна 15 см.

Задание 2.Основанием пирамидыDABC является прямоугольный треугольник ABC, у которого гипотенуза AB равна 25 см, а катет AC равен 24 см. Боковое ребро DA перпендикулярно к плоскости основания и равно 7 см. Найдите площадь боковой поверхности пирамиды.

Задание 3.Основанием пирамиды является прямоугольник со сторонами 5 и 3 см. Ее объем равен

15 см³. Найдите высоту этой пирамиды.

12 Следующая ⇒