- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Предмет: Алгебра и начала анализа (ЕМН)
 ФИО ученика: __________________________
ФИО ученика: __________________________
ФИО учителя: __________________________
Балл:__________________________
Предмет: Алгебра и начала анализа (ЕМН)
Класс 10 «___»
Суммативное оценивание
за раздел «Применение производной» (Сор № 10)
Всего баллов: 16
Критерий оценивания
№
задания
Балл
Использует определение точек
экстремума функции
1(1)
Использует условие возрастания
(убывания) функции и находит промежутки монотонности
1(2a)
Находит точки перегиба графика
функции
1(2b)
Строит график
функции
1(2c)
Решает задачи на нахождение наибольшего (наименьшего) значения функции
Итого
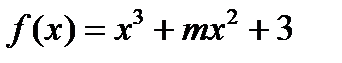 f принимает наименьшее значение, равное
f принимает наименьшее значение, равное 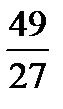 на отрезке
на отрезке 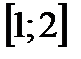 .
.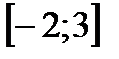 ;
;