ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 14. Краткие теоретические сведения

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 14

Тема: Решение задач на вычисление вероятностей

Краткие теоретические сведения

Определение.Вероятностью события A называется число Р(А), около которого колеблется значение статистической частоты этого события при условии увеличения количества испытаний.

При статистическом определении в качестве вероятности события принимается его относительная частота.

Относительной частотой события 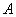называют отношение числа испытаний 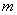, в которых данное событие появилось, к общему числу 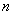фактически проведённых испытаний: .

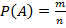Частота события обладает следующими свойствами:

1. Частота случайного события есть число, заключенное между нулем и единицей:
0<P(A)<1

2. Частота достоверного события U равна единице:
P(U)=1

3. Частота невозможного события V равна нулю:
P(V)=0

4. Частота суммы двух несовместных событий A и B равна сумме частот этих событий:
P(A+B)=P(A)+P(B)

Пример.В ящике находится 15 качественных и 5 бракованных деталей. Наудачу извлекаются 2 детали. Найти вероятность того, что:

а) обе детали будут качественными;
б) одна деталь будет качественной, а одна – бракованной;
в) обе детали бракованные.

Решение: всего: 15 + 5 = 20 деталей в ящике. Вычислим общее число исходов:
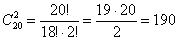способами можно извлечь 2 детали из ящика.
а) Рассмотрим событие: А – обе извлечённые детали будут качественными.
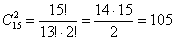способами можно извлечь 2 качественные детали.
По классическому определению вероятности: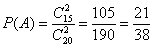
б) Рассмотрим событие: В – одна деталь будет качественной, а одна – бракованной.
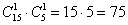способами можно извлечь 1 качественную деталь и 1 бракованную.
По классическому определению: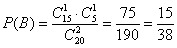
в) Рассмотрим событие: С – обе извлечённые детали бракованные.
способами можно извлечь 2 бракованные детали.
По классическому определению: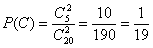
Проверка: вычислим сумму вероятностей событий, образующих полную группу: 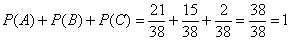, что и требовалось проверить.
Ответ: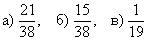

Содержание работы

Вариант 1.

Задача 1.Пусть имеется 60 деталей, среди которых 45 исправленных, а 15 бракованных. Найти вероятность того, что взятая наугад деталь окажется исправной.

Задача 2. В лукошке 16 пирожков: 7 с картошкой, 5 с капустой и 4 с вишней. Катя наугад выбирает два пирожка. Найдите вероятность того, что:

А) оба с вишней

Б) один с картошкой и один с капустой

В) оба с вареньем

Задача 3. В лотерее из 5 000 билетов имеются 25 выигрышных. Вынимают наугад один билет. Чему равна вероятность тому, что билет выигрышный.

Вариант 2.

Задача 1. Из урны, в которой находятся 7 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что шар черный.

Задача 2. В среднем из 200 садовых насосов, поступивших в продажу, 5 подтекают. Наугад выбирают 5 насосов. Найдите вероятность того, что:

А) 3 насоса подтекают и 2 не подтекают

Б) 4 не подтекают и 1 подтекает

В) 5 не подтекают

Задача 3. В ящике 10 белых и 12 черных шаров. Извлекают наудачу один шар. Найти вероятность того, что вынутый шар окажется белым.