
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Равенство векторов.. Примеры задач на равенство векторов. Примеры плоских задач на равенство векторов. Примеры пространственных задач на равенство векторов
Тема: Равенство векторов.
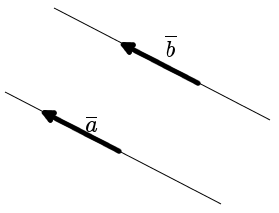
Определение. Вектора a и b называются равными, если они имеют одинаковую длину, лежат на параллельных прямых или на одной прямой, и направлены в одном направлении. (рис. 1).
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b, если a↑↑b и |a| = |b|.
Условие равенства векторов.Вектора равны, если их координаты равны.
|
| рис. 1 |
Примеры задач на равенство векторов
Примеры плоских задач на равенство векторов
Пример 1. Определить какие из векторов равны a = {1; 2}, b = {1; 2}, c = {3; 2}.
Решение:
a = b - так как их координаты равны,
a ≠ c - так как их координаты не равны,
b ≠ c - так как их координаты не равны.
Пример 2. При каком значении параметра n вектора a = {1; 8;} и b = {1; 2n} равны.
Решение:
Проверим равенство компонентов векторов
ax = bx = 1
ay = by => 8 = 2n => n = 8/2 = 4
Ответ: при n = 4 вектора a и b равны.
Примеры пространственных задач на равенство векторов
Пример 3. Определить какие из векторов равны a = {1; 2; 4}, b = {1; 2; 2}, c = {1; 2; 4}.
Решение:
a = c - так как их координаты равны,
a ≠ b - так как их координаты не равны,
b ≠ c - так как их координаты не равны.
Пример 4. При каком значении параметра n вектора a = {1; 2; 4} и b = {1; 2; 2n} равны.
Решение:
Проверим равенство компонентов векторов
ax = bx = 1
ay = by = 2
az = bz => 4 = 2n => n = 4/2 = 2
Ответ: при n = 2 вектора a и b равны.


Выполните домашнее задание:
1.При каком значении параметра n вектора a = {1; 2n; 4} и b = {1; 6; 4} равны.
2.
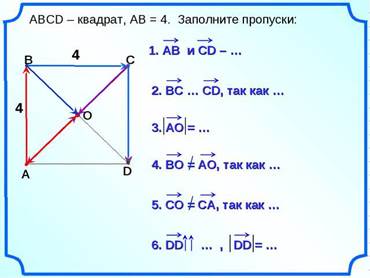
2. 
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|