Решение задач на вычисление объема шара, площади сферы

Решение задач на вычисление объема шара, площади сферы

В III веке до нашей эры жил великий учёный своих дней – Архимед. Он сделал множество открытий, но, согласно легенде, больше всего он гордился тем, что получил соотношение между объёмом цилиндра и объёмом вписанного в этот цилиндр шара. Согласно этой же легенде, на могиле Архимеда, которая не сохранилась до наших дней, был изображен цилиндр и вписанный в него шар, а также написано соотношение объёмов цилиндра и шара.

В то время это было великое достижение, так как точных формул для нахождения объёмов цилиндра и шара ещё не было.

Найдём это соотношение.

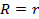, где R – радиус цилиндра; r – радиус шара

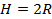, где H – высота цилиндра, так как шар можно вписать только в равносторонний цилиндр.

Объём шара:

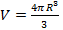
Объём цилиндра:

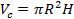
Отношение этих объёмов:

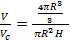
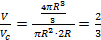
Отношение площадей этих фигур будет таким же. Докажем это. Площадь шара:

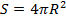
Площадь цилиндра

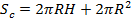
Отношение этих площадей:

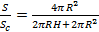
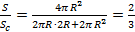
Задачи для самостоятельного решения

Задача 1.Шар, радиус которого 41 дм, пересечён плоскостью на расстоянии 9 дм от центра. Найдите плоскость сечения.

Задача 2.Требуется переплавить в один шар два чугунных шара с диаметрами 25 см и 31 см. Найдите диаметр нового шара.

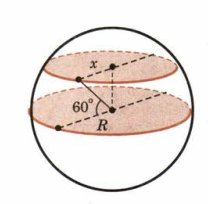
Задача 3.Радиус земного шара 6371 км. Чему равна длина параллели, если её широта 60°?