ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 54. Краткие теоретические сведения. Образец выполнения заданий

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 54

Тема: Решение задач на цилиндр

Краткие теоретические сведения

Площадь полной поверхности цилиндраS_{полн =}S_{бок +}S_осн

Площадь боковой поверхности цилиндраS_бок = 2πrh

Образец выполнения заданий

Задача 1.В нижнем основании цилиндра проведена хорда, длиной 8 см, находящаяся на расстоянии 3 см от центра этого основания. Найти площадь осевого сечения цилиндра, если высота цилиндра равна 6 см.

Дано: цилиндр

AB = 8 см

OH = 3 см

h = OO₁ = AE = DC = 6 см

Найти: S_ACDE

Решение:

1. S_ACDE = AC ∙ DC = AC ∙ 6;

2. Рассмотрим ∆AOB, OB = OA = r, значит треугольник равнобедренный. OH – высота этого треугольника и медиана.

AH = BH = 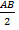= 8:2 = 4 (см)

3. Из ∆AOH – прямоугольного, по теореме Пифагора выразим AO:

AO² = AH² + HO² = 4²+ 3² = 16 + 9 = 25

AO= 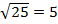(см)

4. AC – диаметр окружности, AC = 2AO = 2∙ 5 = 10 (см)

5. S_ACDE = AC ∙ 6 = 10∙ 6 = 60 (см²)

Ответ: 60 см²

Задача 2.Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 60° и равна 20 см. Найдите площадь боковой поверхности цилиндра.

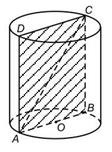Дано: цилиндр

AC = 20 см

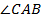= 60°

Найти: S_бок

Решение:

1. S_бок = 2πrh

2. Рассмотрим ∆ABC – прямоугольный, 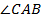= 60°

= 90° - 60° = 30° (так как сумма острых углов в прямоугольном треугольнике равна 90°)

3. AB = AC : 2 = 20 : 2 = 10 (по свойству катета лежащего против угла в 30°)

4. r = AB : 2 = 10 : 2 = 5 (см)

5. Из ∆ABC – прямоугольного, по теореме Пифагора выразим BC:

BC² = AC² – AB² = 20² – 10² = 400 – 100 = 300

BC = 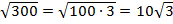(cм)

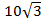BC = h = (cм)

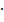
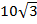6. S_бок = 2πrh = 2π 5 = 100 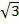π (см²)

Ответ: 100 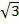π см²

Содержание работы

Вариант 1.

Задача 1. В нижнем основании цилиндра проведена хорда, длиной 24 см, находящаяся на расстоянии 5 см от центра этого основания. Найти площадь осевого сечения цилиндра, если высота цилиндра равна 10 см.

Задача 2. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 60° и равна 24 см. Найдите площадь боковой поверхности цилиндра.

Вариант 2.

Задача 1. В нижнем основании цилиндра проведена хорда, длиной 30 см, находящаяся на расстоянии 8 см от центра этого основания. Найти площадь осевого сечения цилиндра, если высота цилиндра равна 5 см.

Задача 2. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 60° и равна 18 см. Найдите площадь боковой поверхности цилиндра.

12 Следующая ⇒