Хелпикс

Главная

Контакты

Случайная статья



Практическое занятие №13. Применение производной к исследованию функции. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИЙ И ПОСТРОЕНИ ИХ ГРАФИКОВ. ДОСТАТОЧНЫЙ ПРИЗНАК ВОЗРАСТАНИЯ ФУНКЦИИ. ДОСТАТОЧНЫЙ ПРИЗНАК УБЫВАНИЯ ФУНКЦИИ. ДОСТАТОЧНЫЕ УСЛОВИЯ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА



Практическое занятие №13

Применение производной к исследованию функции

 

Цель:  Научиться применять правило применения производной к исследованию функций на промежутки монотонности и экстремумы при исследовании конкретных функций.

 

Теоретическая часть с примерами:

 

ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИЙ И ПОСТРОЕНИ ИХ ГРАФИКОВ

  1. Найти область определения функции
  2. Определить четность, нечетность функции
  3. Определить периодичность функции
  4. Найти промежутки монотонности функции
  5. Найти экстремумы функции
  6. Определить при необходимости дополнительные точки графика функции
  7. Найти область значения функции
  8. Построить график функции

  

ДОСТАТОЧНЫЙ ПРИЗНАК ВОЗРАСТАНИЯ ФУНКЦИИ

Если производная функции положительна в каждой точке некоторого промежутка, то функция возрастает на данном промежутке

 

ДОСТАТОЧНЫЙ ПРИЗНАК УБЫВАНИЯ ФУНКЦИИ

Если производная функции отрицательна в каждой точке некоторого промежутка, то функция убывает на данном промежутке.

 

 

ДОСТАТОЧНЫЕ УСЛОВИЯ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА В ТОЧКЕ (ТОЧКА МАКСИМУМА И ТОЧКА МИНИМУМА)

Если функция непрерывна в некоторой точке и слева от неё производная функции имеет знак «+», а справа от неё производная имеет знак «-», то данная точка является точкой максимума функции на данном промежутке.

 

Если функция непрерывна в некоторой точке и слева от неё производная функции имеет знак «-», а справа от неё производная имеет знак «+», то данная точка является точкой минимума функции на данном промежутке.

 

Пример:  Определить промежутки возрастания (убывания) точки минимума, максимума следующих функций:

       2.1.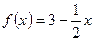

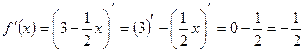
т.к. 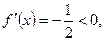 то функция убывает на всей оси ОДЗ.

 

       2.2.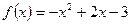

                 

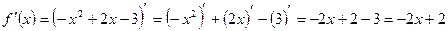
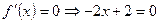
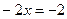
                       -критическая точка.

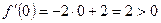
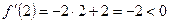
Функция возрастает на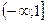

Функция убывает на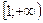

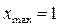
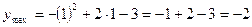
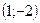- точка максимума.

 

2.3.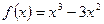

              

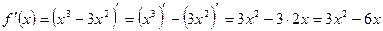
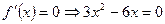
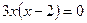
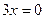            или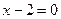

                  х = 0    х = 2 - критические точки

 

2.4.

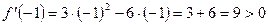
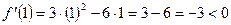
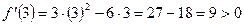
Функция возрастает на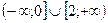

Функция убывает на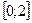

                                          

                      

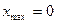
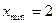
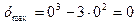
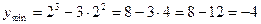
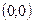- точка максимума  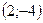           - точка минимума

 

Практические задания

  1. Исследовать функцию на промежутки монотонности и экстремумы функции:

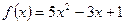
  1. определить промежутки возрастания функции и точку минимума:

 

           

 

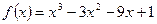
Оценка: «3» - задание 1

         «4 и 5» - задание 1,2

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.