Экзаменационная программа. по дисциплине «Математика». ЮР, 1 курс, 2-й семестр, 2020 г.

Экзаменационная программа

по дисциплине «Математика»

ЮР, 1 курс, 2-й семестр, 2020 г.

Первообразная. Ее свойства.
Неопределенный интеграл. Его свойства.
Замена переменной в неопределенном интеграле. Интегрирование по частям.
Определенный интеграл. Его свойства и геометрический смысл.
Замена переменной в определенном интеграле. Интегрирование по частям для определенного интеграла.
Геометрическое приложение определенного интеграла (вычисление площадей, объемов и длин дуг).
Несобственные интегралы 1-го и 2-го рода. Признаки сходимости несобственных интегралов 1-го рода.
Определение предела ФНП. Частные производные функции многих переменных, правила их вычисления.
Частные производные высших порядков. Теорема о равенстве смешанных производных.
Экстремум функции нескольких переменных. Необходимые условия экстремума. Достаточные условия экстремума.
Понятие двойного интеграла. Его свойства. Геометрический смысл двойного интеграла.
Сведение двойного интеграла к повторному.
Замена переменной в двойном интеграле. Полярная система координат, вычисление двойного интеграла в полярных координатах.
Геометрические и физические приложения двойных интегралов.
Понятие обыкновенного дифференциального уравнения (ДУ). Частное и общее решения, частный и общий интегралы дифференциального уравнения. Интегральные кривые.
Задача Коши для ДУ 1-го порядка. Геометрический смысл ДУ 1-го порядка. Теорема Коши о существовании и единственности решения ДУ.
ДУ с разделяющимися переменными. Неполные дифференциальные уравнения.
Однородные функции. Интегрирование однородного ДУ уравнения первого порядка.
Линейное ДУ уравнение первого порядка, нахождение его решения. Метод вариации постоянной.
Решение ДУ в полных дифференциалах.
Дифференциальные уравнения второго порядка. Задача Коши и её геометрический смысл. Теорема о существовании и единственности решения задачи Коши для ДУ 2-го порядка.
Дифференциальные уравнения второго порядка, допускающие понижение порядка.
Линейные ДУ второго порядка. Однородные линейные ДУ (ОЛДУ) второго порядка. Линейно зависимые и независимые функции на отрезке. Определитель Вронского и его свойства. Структура общего решения ОЛДУ.
Неоднородные линейные ДУ второго порядка. Структура его общего решения. Метод Лагранжа вариации постоянных для НЛДУ второго порядка.
ОЛДУ второго порядка с постоянными коэффициентами, Построение его общего решения по корням характеристического уравнения.
Неоднородные линейные ДУ второго порядка с правой частью специального вида..
Понятие числового ряда и его суммы. Сходимость ряда. Геометрический ряд. Необходимое условие сходимости. Свойства сходящихся числовых рядов.
Знакоположительные ряды. Гармонический ряд, ряд Дирихле. Признаки сравнения.
Признаки сходимости рядов с неотрицательными членами: признак Даламбера, радикальный и интегральный признаки Коши.
Знакопеременные числовые ряды. Абсолютная сходимость. Знакочередующиеся ряды. Признак Лейбница.
Функциональный ряд. Сумма ряда. Область сходимости.
Степенной ряд. Теорема Абеля. Интервал и радиус сходимости степенного ряда. Формула радиуса сходимости степенного ряда.
Ряд Тейлора. Теорема о разложимости функции в ряд Тейлора и Маклорена. Разложение в ряд Маклорена элементарных функций: 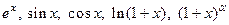. Приближенное вычисление интегралов.