Об умножении вероятностей

Группа 7-18 Согласовано

Дата_07.04.2020 Зам. директора по УВР___________Татаринова В.Д

Урок № 92-93

Тема: Теория вероятностей. Умножение вероятностей.

или

Об умножении вероятностей

Пусть происходят два несовместных события А и В, их вероятности соответственно равны Р(А) и Р(В). Произведением двух событий А и В называют событие А·В, которое состоит в совместном появлении этих событий. Вычисляется по формуле:

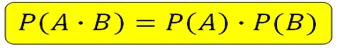
*Умножение означает, что при некоторых обстоятельствах наступит и событие А, и событие В.

Пример с той же игральной костью:

Бросаем игральную кость два раза. Какова вероятность выпадения двух шестёрок?

Вероятность выпадения шестёрки первый раз равна 1/6. Во второй раз так же равна 1/6. Вероятность выпадения шестёрки и в первый раз и во второй раз равна произведению вероятностей:

Говоря простым языком: когда в одном испытании происходит некоторое событие, и ПРИ ЭТОМ происходит(ят) другое (другие), то вероятности этих событий перемножаются.

Задачи с игральной костью мы решали, но пользовались только логическими рассуждениями, формулу произведения не использовали. В рассматриваемых же ниже задачах без формул не обойтись, вернее с ними будет получить результат проще и быстрее.

Стоит сказать ещё об одном нюансе. При рассуждениях в решении задач используется понятие ОДНОВРЕМЕННОСТЬ совершения событий. События происходят ОДНОВРЕМЕННО — это не означает, что они происходят в одну секунду (в один момент времени). Это значит, что они происходят в некоторый промежуток времени (при одном испытании).

Например:

Две лампы перегорают в течение года (может быть сказано — одновременно в течение года)

Два автомата ломаются в течении месяца (может быть сказано — одновременно в течение месяца)

Игральная кость бросается три раза (очки выпадают одновременно это означает при одном испытании)

Биатлонист делает пять выстрелов. События (выстрелы) происходят во время одного испытания.

События А и В являются НЕзависимыми, если вероятность любого из них не зависит от появления либо непоявления другого события.

12 Следующая ⇒