Тема: Основные понятия равносильности неравенств на множестве. Возведение неравенств в четную степень

Тема: Основные понятия равносильности неравенств на множестве. Возведение неравенств в четную степень

Цель: ввести понятия равносильных неравенств на множествах; перечислить основные преобразования, приводящие к неравенствам, равносильным на множествах; научиться решать неравенства путем замены его равносильным неравенством на множестве.

Запишите определения и основные понятия.

Основные понятия:

Пусть даны два неравенства f(x)> g(x) и p(x)>h(x) и пусть дано некоторое множество чисел М. Если любое решение первого неравенства, принадлежащее множеству М, является решением второго неравенства, а любое решение второго неравенства, принадлежащее множеству М, является решением первого неравенства, то такие неравенства называют равносильными на множестве М.

Если каждое из этих неравенств не имеет решений на множестве М , то такие неравенства называются равносильными на множестве М.

Определения:

Замену одного неравенства другим неравенством, равносильным ему на множестве М, называют равносильным переходом на множестве М от одного неравенства к другому. Если два неравенства равносильны на множестве всех действительных чисел, то в таких случаях говорят, что неравенства равносильны, опуская слова на множестве действительных чисел.

Например, неравенства

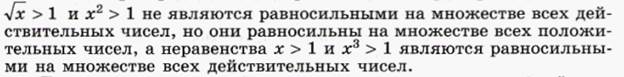
Основные преобразования неравенств, приводящие исходное неравенство к неравенству, равносильному ему на некотором множестве чисел

12 Следующая ⇒