Контакты

Случайная статья

Основное свойство дроби

С помощью дробей одну и ту же часть целого предмета можно записать разными способами.

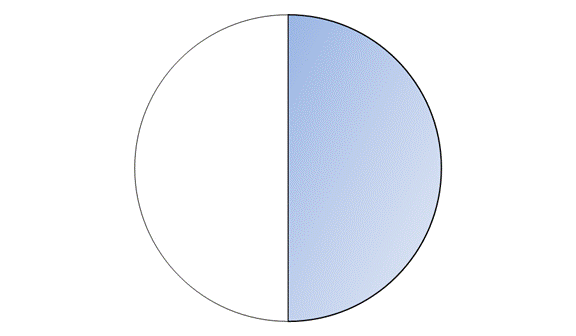
На рисунке закрашена половина круга

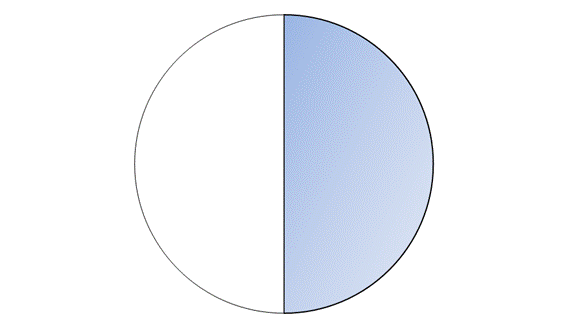
Если этот же круг разделить на 4 части, то эту же половину круга можно представить как

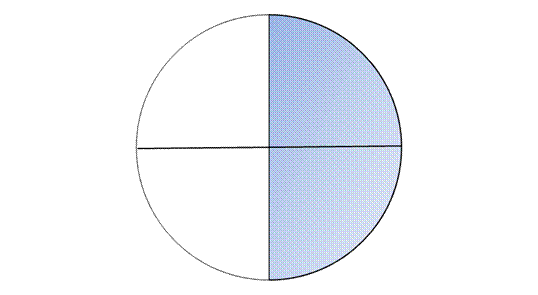
Если этот же круг разделить на 8 частей, то эту же половину круга можно представить как

.

Таким образом, все эти дроби равны.

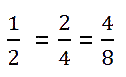
Дробь

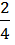мы получили из дроби 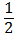, умножив её числитель и знаменатель на 2.

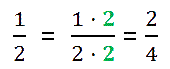
А чтобы получить , мы числитель и знаменатель умножили на 4.

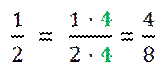
Для удобства дополнительный множитель записывают на наклонной черте справа над дробью .

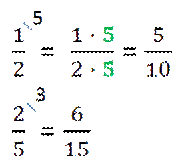
Вернёмся ещё раз к нашим дробям и запишем их в другом порядке.

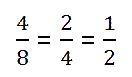
Запомните!

Дробь, равную данной, можно получить, если числитель и знаменатель дроби одновременно разделить на одно и то же число, не равное нулю.

Такое преобразование дроби называют сокращением дроби.

Сокращение дроби обычно записывают следующим образом.

Числитель и знаменатель зачёркиваются чёрточками, и рядом с ними записываются результаты деления (частные) числителя и знаменателя на одно и то же число.

Число, на которое делили числитель и знаменатель, держим в уме.

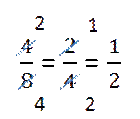
В нашем примере мы сокращали (то есть делили и числитель, и знаменатель) дробь на двойку, которую держали в уме.

Сокращение дроби можно проводить последовательно.

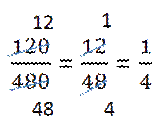
Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.