
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание на вторник: запишите ответы на тест, свой вариант.
Задание на вторник: запишите ответы на тест, свой вариант.
А – 11 Тест по теме: «Площадь криволинейной трапеции» В - 1
ОБВЕДИТЕ КРУЖКОМ НОМЕР ПРАВИЛЬНОГО ОТВЕТА:
1. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ – ЭТО ФИГУРА, ОГРАНИЧЕННАЯ ГРАФИКОМ
1) непрерывной на отрезке [a;b] функции f(x)
2) непрерывной и не меняющей на отрезке [a;b] знака функции f(x)
3) непрерывной и не меняющей на отрезке [a;b] знака функции f(x), прямыми x=a, x=b
4) непрерывной и не меняющей на отрезке [a;b] знака функции f(x), прямыми x=a, x=b, отрезком [a;b]
2. ФИГУРА, НЕ ЯВЛЯЮЩАЯСЯ КРИВОЛИНЕЙНОЙ ТРАПЕЦИЕЙ, ИЗОБРАЖЕНА НА РИСУНКЕ
 |
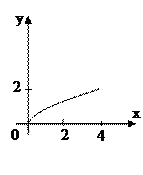 3. ИЗОБРАЗИТЕ НА РИСУНКЕ НЕДОСТАЮЩУЮ ЛИНИЮ, ОГРАНИЧИВАЮЩУЮ КРИВОЛИНЕЙНУЮ ТРАПЕЦИЮ С ПЛОЩАДЬЮ
3. ИЗОБРАЗИТЕ НА РИСУНКЕ НЕДОСТАЮЩУЮ ЛИНИЮ, ОГРАНИЧИВАЮЩУЮ КРИВОЛИНЕЙНУЮ ТРАПЕЦИЮ С ПЛОЩАДЬЮ 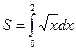
|
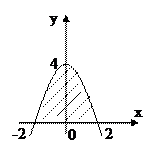 4. ПЛОЩАДЬ ИЗОБРАЖЕННОЙ НА РИСУНКЕ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ _____________
4. ПЛОЩАДЬ ИЗОБРАЖЕННОЙ НА РИСУНКЕ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ _____________
СООТНЕСИТЕ СТРЕЛКОЙ:
5. ФУНКЦИЯ f(x) ПЕРВООБРАЗНАЯ F(x)
1) 3x2 A) 
2)  B)
B) 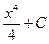
3) 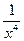 C)
C) 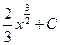
4) x3 D) 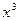 +C
+C
А – 11 Тест по теме: «Площадь криволинейной трапеции» В - 2
ОБВЕДИТЕ КРУЖКОМ НОМЕР ПРАВИЛЬНОГО ОТВЕТА:
1. На каком рисунке изображена фигура, не являющаяся криволинейной трапецией?

2. С помощью формулы Ньютона-Лейбница вычисляют:
А. Первообразную функции; Б. Площадь криволинейной трапеции; В. Интеграл; Г. Производную.
3. Найдите площадь заштрихованной фигуры:

А. 0; Б. –2; В. 1; Г. 2.
4. Найдите площадь фигуры ограниченной осью Ох и параболой у = 9 – х2
А. 18; Б. 36; В. 72; Г. Нельзя вычислить.
5. Найдите площадь фигуры, ограниченной графиком функции у = sin x, прямыми х = 0, х = 2 и осью абсцисс.
А. 0; Б. 2; В. 4; Г. Нельзя вычислить.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|