Задания для построения

ПРАКТИЧЕСКАЯ РАБОТА

«ПОСТРОЕНИЕ ЛЕКАЛЬНЫХ КРИВЫХ»

Цель работы: Ознакомление студентов с различными видами лекальных кривых, их применением в различных деталях машин и механизмов, а также приобретение навыков построения и вычерчивания контуров деталей с применением лекальных кривых.

Содержание работы

1. Ознакомиться с методическими указаниями к работе.

2. В соответствии с заданием вычертить в рабочей тетради (на отдельных листках в клетку, чтобы потом вставить в тетрадь) спираль Архимеда, эллипс, чертеж кронштейна, с применением построения параболы..

В машиностроительном черчении часто приходится прибегать к вычерчиванию кривых, состоящих из ряда сопряженных частей, которые невозможно провести циркулем. Лекальные кривые строят обычно по ряду принадлежащих им точек, которые затем соединяют плавной линией от руки и обводят толстой основной линией, используя лекало (рисунок 1)

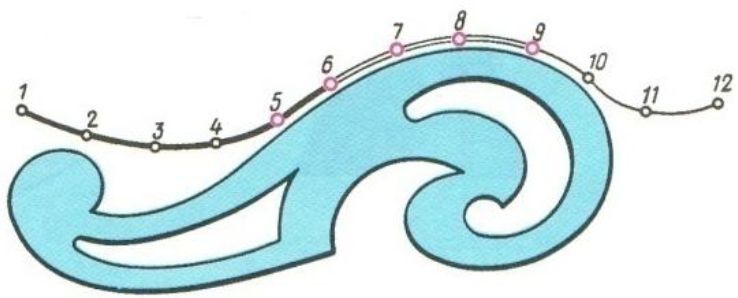
Рисунок 1 - Лекало

При сечении прямого кругового конуса плоскостями, различно расположенными по отношению к осям конуса, получаются контуры сечения, образующие эллипс, параболу и гиперболу (рисунок 2).

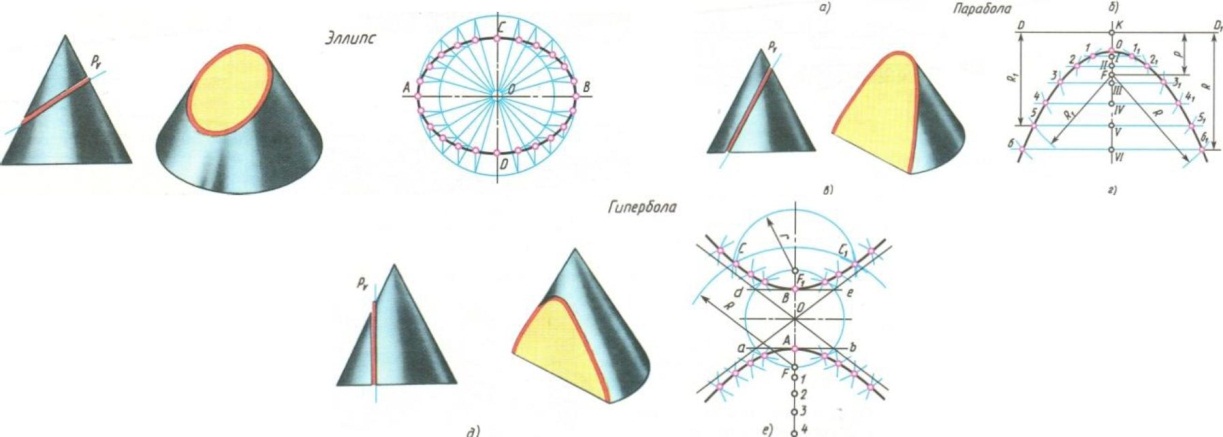
Рисунок 2 – Кривые конических сечений

Эллипс — плоская замкнутая кривая. При пересечении конуса или цилиндра наклонной плоскостью в сечении получается эллипс.

Построение лекальной кривой – эллипса

1.Даны большая ось АВ и малая ось CD эллипса

2. Проводим из центра О окружность радиуса ОА и окружность радиуса ОС.

3. Делим большую окружность на 12 равных частей. Точки деления 1, 2, 3, 12 окружности соединяем с центром О. Прямые 1-7, 2-8 ... 6-12 делят малую окружность тоже на 12 равных частей.4. Из точек деления большой окружности проводим прямые параллельные CD. Из точек деления малой окружности проводим прямые, параллельные АВ. Точки пересечения вертикальных и горизонтальных прямых – это искомые точки эллипса. 5. Соединяем точки плавной кривой с помощью лекал (рисунок 3.).

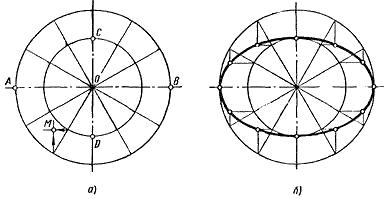
Рисунок 3 - Построение лекальной кривой – эллипса

Спираль Архимеда - плоская кривая, полученная как след точки, движущейся равномерно поступательно от неподвижной точки О по выходящему из нее и равномерно вращающемуся вокруг точки О лучу (радиусу) Точка О называется полюсом спирали; отрезок ОА называется шагом t спирали; отрезок KL – нормалью спирали, а прямая MN, перпендикулярная к нормали, называется касательной; точка К может находиться в любом месте спирали, а точку L находят путем построения, для чего точку К соединяют прямой с точкой О и в точке О проводят перпендикуляр к отрезку КО, который пересечет в точке L окружность, проведенную из центра О диаметром D = t/3,14.

Построение Архимедовой спирали

Заданный шаг t спирали Архимеда делят на несколько, например на восемь, равных частей. Из конца О отрезка / проводят окружность R = t и делят ее на столько же равных частей, на сколько был разделен шаг t.

На первом луче путем проведения дуги радиусом O1 из центра О получают точку I, на втором луче путем проведения дуги радиусом O2 получают точку II и т.д.

После того как на всех лучах будут получены точки I, II, III, IV, V, VI, VII и VIII, проводят через них кривую – спираль Архимеда.

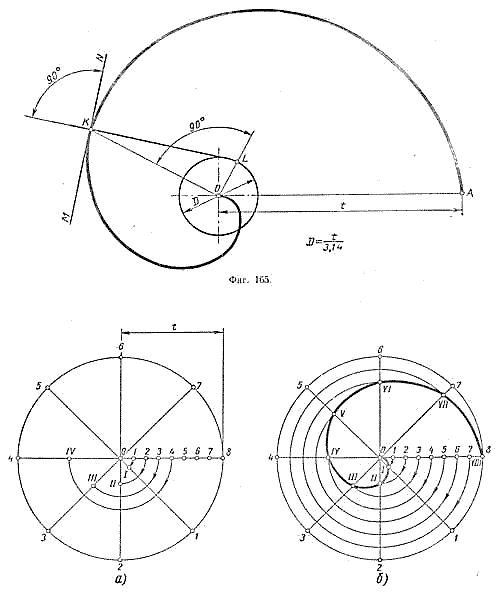
Рисунок 4 - Построение лекальной кривой – Спирали Архимеда

Задания для построения

12 Следующая ⇒