ПО «Математическому моделированию»

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Гжельский государственный университет»(ГГУ)

Колледж ГГУ

Специальность 09.02.07 Информационные системы и программирование

Отчет

ПО «Математическому моделированию»

ВЫПОЛНИЛ:

Студент группы ИСП-О-18

Вдовин А.В.

ПРОВЕРИЛА:

Шелепова Т.С.

Оценка ___________________

п. Электроизолятор

2020 г.

Пр.19 «Решение матричной игры методом итераций»

Цель:

Отработать и закрепить умения находить решение матричной игры методом итераций.

Вариант №7

Дана платежная матрица игры. Решить матричную игру методом итераций:

1. Определить оптимальные смешанные стратегии игроков А и В

2. Определить цену игры

Провести не менее 800 шагов итерационного процесса.

Проверить найденное решение с помощью сведения к задаче линейного программирования и надстройки MS Excel "Поиск решения".

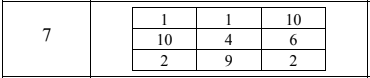
Найдем нижнюю и верхнюю цену игры:

a = max(1;4;2) = 4

b = min(10;10;9) = 9

Цена игры:

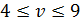
Убедившись в отсутствии седловой точки, разработаем процедуру нахождения решения игры методом итераций.

Каждая партия включает пару выборов — стороны A и стороны B. Они помещены в столбцах 2 и 6.

Накопленные к k-му шагу процесса проигрыши стороны B для каждой из ее стратегий помещены в столбцах 3—5; в столбцах 7—9 помещены накопленные выигрыши стороны A. В каждой строчке подчеркнуты минимальный проигрыш стороны B и максимальный выигрыш стороны A. Именно они определяют выбор соответствующей стороной стратегии для очередной партии игры. Если выделить сразу несколько выигрышей (проигрышей), то выбор стратегий осуществляется с использованием, например, случайного розыгрыша.

В столбцах 10 и 11 помещены средние значения соответственно нижней (α̃k) и верхней (β̃k) цены игры. Параметр α̃k получается делением минимального накопленного проигрыша стороны B на число проведенных партий k, параметр β~k — делением максимального выигрыша стороны A на число проведенных партий k игры.

В столбце 12 помещены средние значения цены игры ṽk , для k-го шага итерационного процесса. Они вычислены как среднее арифметическое значение:

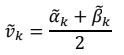
Подсчитывая число случаев применения стороной каждой стратегии и, деля его на число партий k, получим статистические оценки частностей p̃i(k), q̃j(k) применения сторонами всех стратегий Ai, Bj.

Получаемые в результате итерационного процесса средние значения цены игры ṽk и смешанные стратегии сходятся к истинным значениям.

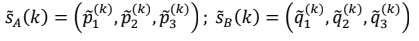
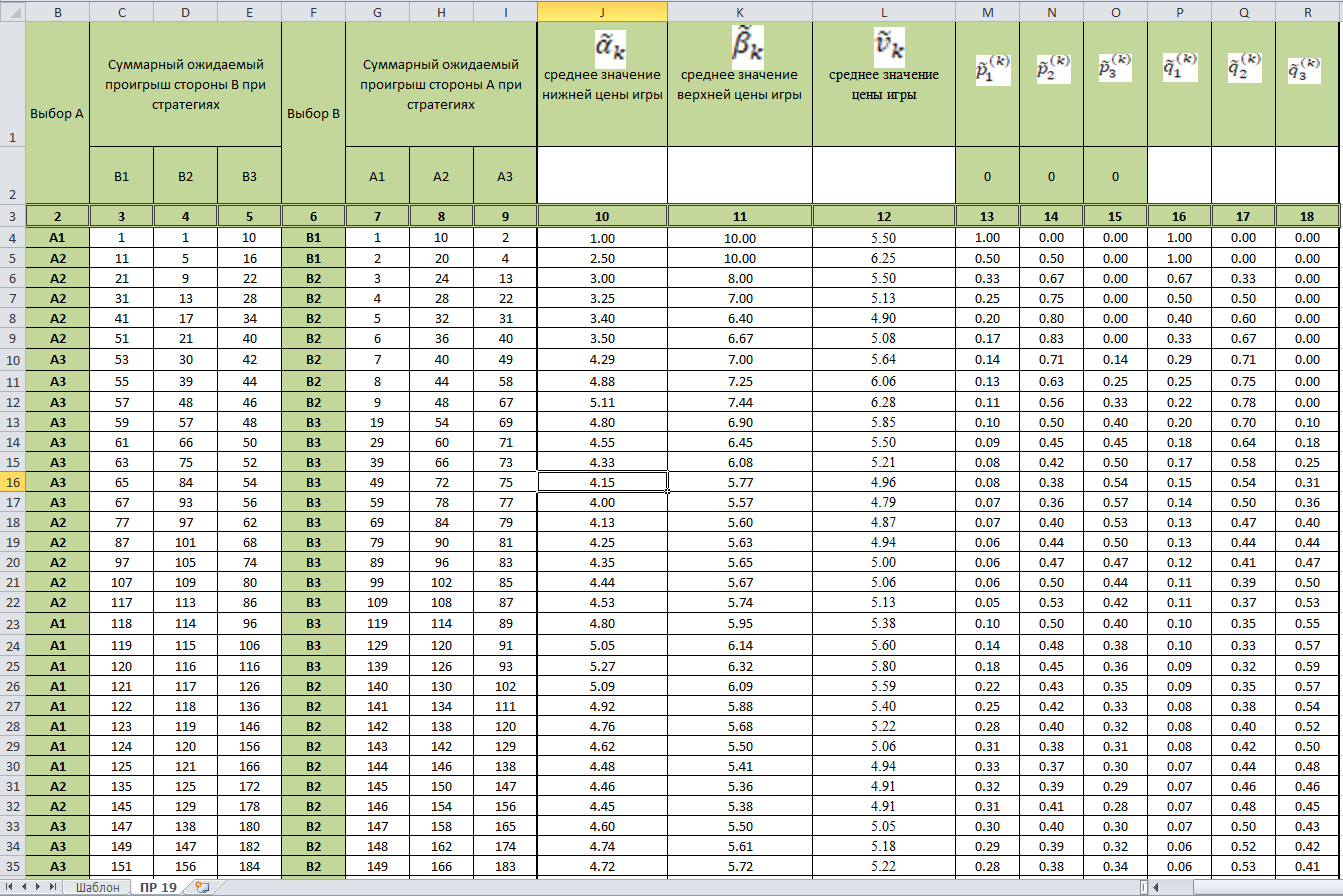
Допустим, что на первом шаге итерационного процесса стороны избрали стратегии А1 и В1.

Используем матрицу и запишем в таблицу проигрыши стороны В и выигрыш стороны А.

Как видно, минимальный проигрыш стороны В на первом шаге имеет место при использовании стратегии В1. Эту стратегию сторона В будет использовать на следующем шаге процесса.

Максимальный выигрыш сторона А на первом шаге имеет при использовании стратегии А3. Эту стратегию сторона А будет использовать на следующем шаге.

Далее заполним столбцы 10-18:

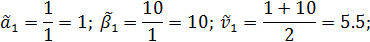
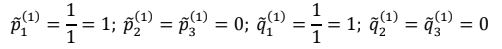
Переходим ко второму шагу процесса. В столбцах 2 и 6 запишем избранные сторонами стратегии. Используя матрицу, запишем в столбцах 3-5 и 7-9 проигрыши В и выигрыши А за 2 шага. Определим оптимальные стратегии сторон для 3 шага. Ими являются А2 и В2. Затем определим:

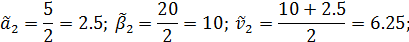
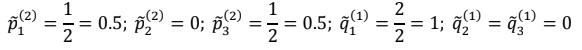
Переходим к 3-у шагу процесса. В столбцах 2 и 6 запишем избранные сторонами стратегии. Используя матрицу, запишем в столбцах 3-5 и 7-9 проигрыши В и выигрыши А за 3 шага. Определим оптимальные стратегии сторон для 4 шага. Ими являются А2 и В2. Затем определим:

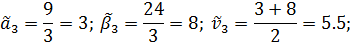
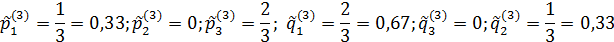
Подобным образом процесс продолжается и далее.

1.1Для первого игрока составим задачу линейного программирования. Применение первым игроком оптимальной стратегии должно обеспечивать ему при любых действиях второго игрока выигрыш не меньше цены игры v:

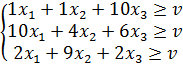
Величина v неизвестна, однако можно считать, что цена игры v > 0. Преобразуем систему ограничений, разделив все члены неравенств на v:

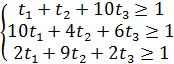
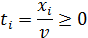
По условию х1 + х2 + х3 = 1. Разделим обе части этого равенства на v:

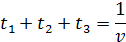
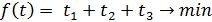
Таким образом, имеем задачу линейного программирования.

1.2 Аналогично для второго игрока составим задачу линейного программирования (двойственная задача):

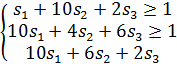, где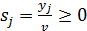

Оптимальная стратегия игрока В должна минимизировать величину v, следовательно, функция:

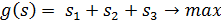
1. Решение задачи линейного программирования

Найдем решение с помощью надстройки Excel Поиск решения.

Воспользуемся надстройкой Поиск решения.

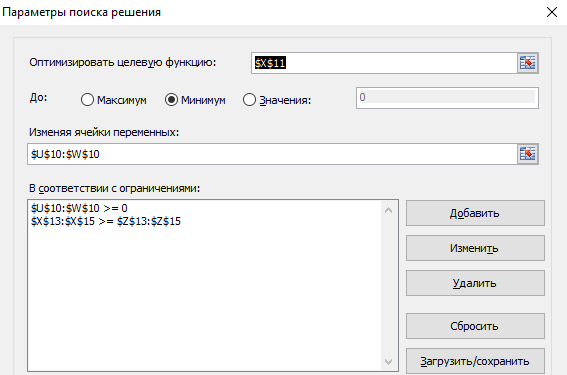
Результат решения

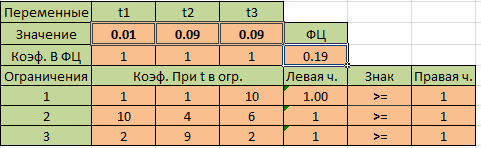
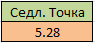
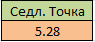
Находим значение седловой точки (цена игры):

Находим оптимальные стратегии первого игрока:

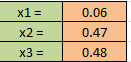
Если первый игрок с вероятностью 0,06 будет применять первую стратегию, а вторую с вероятностью 0,47 и третью с вероятностью 0,48, то при достаточно большом количестве игр с данной матрицей его выигрыш в среднем составит не менее 5,28.

2.1Решение задачи линейного программирования

Найдем решение с помощью надстройки Excel Поиск решения.

Воспользуемся надстройкой Поиск решения.

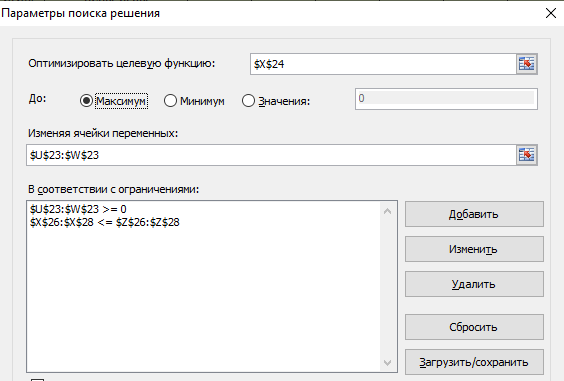
Результат решения:

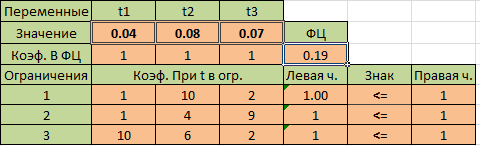
Находим значение седловой точки (цена игры):

Находим оптимальные стратегии первого игрока:

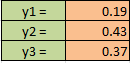
Если второй игрок с вероятностью 0,19 будет применять первую стратегию, вторую стратегию он применит с вероятностью 0,43, а третью с вероятностью 0,37, то при достаточно большом количестве игр с данной матрицей его выигрыш в среднем составит не менее 5,28.