
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Свойства параллельных сечений в пирамиде
МНОГОГРАННИКИ
Свойства параллельных сечений в пирамиде
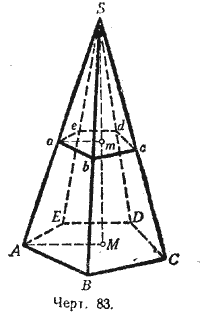
Теорема 1. Если пирамида пересечена плоскостью, параллельной основанию, то:
1) боковые рёбра и высота делятся этой плоскостью на пропорциональные части;
2) в сечении получается многоугольник (abcde), подобный основанию;
3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Замечание. Если обозначить площади основания и сечения пирамиды
соответсвенно через 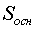 и
и 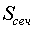 , а их расстояния до вершины через
, а их расстояния до вершины через 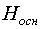 и
и 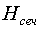 , то
, то 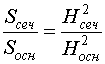
Следствие. У правильной усечённой пирамиды верхнее основание есть правильный многоугольник, подобный нижнему основанию, а боковые грани суть равные и равнобочные трапеции (черт. 83).
Высота любой из этих трапеций называется апофемой правильной усечённой пирамиды.
Теорема 2. Если две пирамиды с равными высотами рассечены на одинаковом расстоянии от вершины плоскостями, параллельными основаниям, то площади сечений пропорциональны площадям оснований.
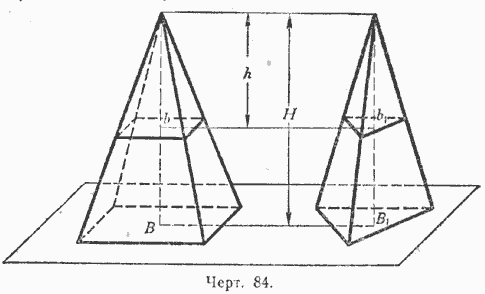
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|