
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Прямоугольная система координат в пространстве.
Прямоугольная система координат в пространстве.
План
1. Прямоугольная система координат в пространстве.
2. Расстояние между точками
3. Координаты середины отрезка
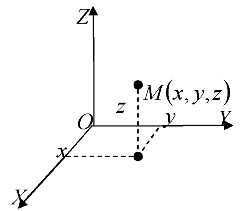 Вопрос 1. Прямоугольная система координат в пространстве.
Вопрос 1. Прямоугольная система координат в пространстве.
Если через точку О в пространстве мы проведем три перпендикулярные прямые, назовем их, выберем направление, обозначим единичные отрезки, то мы получим прямоугольную систему координат в пространстве. Оси координат называются так: Ох – ось абсцисс, Оy – ось ординат и Оz – ось аппликат. Вся система координат обозначается – Oxyz. Таким образом, появляются три координатные плоскости: Оxy, Оxz, Оyz.
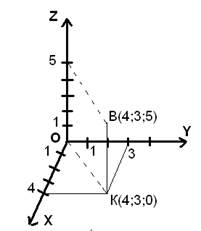 Пример построения точки В(4;3;5) в прямоугольной системе координат:
Пример построения точки В(4;3;5) в прямоугольной системе координат:
 Первая координата точки B – 4, поэтому откладываем на Ox 4, проводим прямую параллельно оси Oy до пересечения с прямой, проходящей через у=3. Таким образом, мы получаем точку K. Эта точка лежит в плоскости Oxy и имеет координаты K(4;3;0). Теперь нужно провести прямую параллельно оси Oz. И прямую, которая проходит через точку с аппликатой 5 и параллельна диагонали параллелограмма в плоскости Oxy. На их пересечении мы получим искомую точку B.
Первая координата точки B – 4, поэтому откладываем на Ox 4, проводим прямую параллельно оси Oy до пересечения с прямой, проходящей через у=3. Таким образом, мы получаем точку K. Эта точка лежит в плоскости Oxy и имеет координаты K(4;3;0). Теперь нужно провести прямую параллельно оси Oz. И прямую, которая проходит через точку с аппликатой 5 и параллельна диагонали параллелограмма в плоскости Oxy. На их пересечении мы получим искомую точку B.
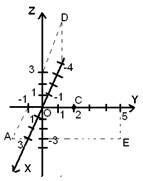
Рассмотрим расположение точек, у которых одна или две координаты равны.
Например, точка A(3;-1;0). Нужно продолжить ось Oy влево до значения -1, найти точку 3 на оси Ox, и на пересечении линий, проходящих через эти значения, получаем точку А. Эта точка имеет аппликату 0, а значит, она лежит в плоскости Oxy.
Точка C(0;2;0) имеет абсциссу и аппликату 0 – не отмечаем. Ордината равна 2, значит точка C лежит только на оси Oy, которая является пересечением плоскостей Oxy и Oyz.
Чтобы отложить точку D(-4;0;3) продолжаем ось Ox назад за начало координат до точки -4. Теперь восстанавливаем из этой точки перпендикуляр – прямую, параллельную оси Oz до пересечения с прямой, параллельной оси Ox и проходящей через значение 3 на оси Oz. Получаем точку D(-4;0;3). Так как ордината точки равна 0, значит точка D лежит в плоскости Oxz.
Следующая точка E(0;5;-3). Ордината точки 5, аппликата -3, проводим прямые проходящие через эти значения на соответствующих осях, и на их пересечении получаем точку E(0;5;-3). Эта точка имеет первую координату 0, значит она лежит в плоскости Oyz.
Вопрос 2. Расстояние между точками
Выразим расстояние между двумя точками 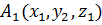 и
и 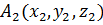 через координаты этих точек.
через координаты этих точек.
Рассмотрим сначала случай, когда прямая  не параллельна оси z.
не параллельна оси z.
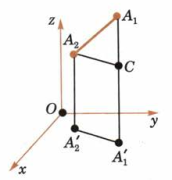
Проведём через точки  и
и 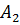 прямые, параллельные оси z. Они пересекут плоскость в точках
прямые, параллельные оси z. Они пересекут плоскость в точках 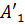 и
и 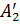 . Эти точки имеют те же координаты x, y, что и точки
. Эти точки имеют те же координаты x, y, что и точки 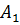 и
и 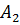 , а координата z у них равна нулю. Проведём теперь плоскость через точку
, а координата z у них равна нулю. Проведём теперь плоскость через точку 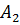 , параллельную оси xy. Она пересечёт прямую
, параллельную оси xy. Она пересечёт прямую 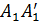 в некоторой точке C. По теореме Пифагора
в некоторой точке C. По теореме Пифагора 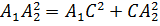 . Отрезки
. Отрезки 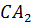 и
и 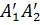 равны, а
равны, а 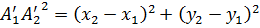 . Длина отрезка
. Длина отрезка 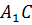 равна
равна 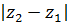 . Поэтому
. Поэтому 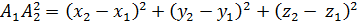 . Если отрезок
. Если отрезок 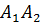 не параллелен оси z, то
не параллелен оси z, то 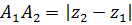 . Тот же результат даёт полученная формула, так как в этом случае
. Тот же результат даёт полученная формула, так как в этом случае 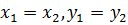 .
.
Расстояние между двумя точками вычисляется по формуле
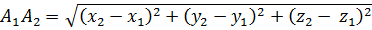
Вопрос 3.Координаты середины отрезка
Середина отрезка - это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.
В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах о поиске медианы или средней линии.
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
То есть координаты середины отрезка с концами 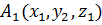 и
и 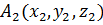 вычисляются по формулам:
вычисляются по формулам:
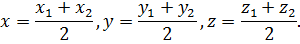
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|