Определение реакций опор с помощью принципа Даламбера

Задача 2

Определение реакций опор с помощью принципа Даламбера

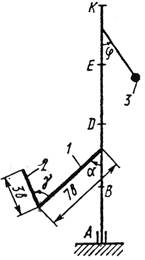
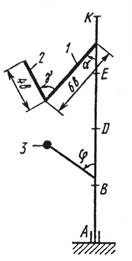
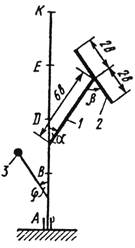
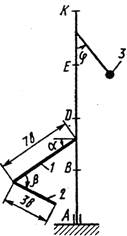
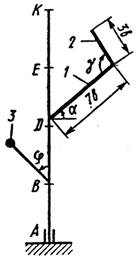
Вертикальный вал АК (рис.0 – 9), вращающийся с постоянной угловой скоростью w (с^-'), закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. № 1 в столбце 2 (АВ = BD == DE = ЕК = а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m1 = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b = 0,2 м, а их массы m₁ и т₂ пропорциональны длинам), и стержень массой m2 и длиной l = 4b с точечной массой т₃(кг) на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы a, b, g, j даны в столбцах 5–8.

Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах а (м).

Таблица № 1

Номер условия выбирается по предпоследней цифре номера зачетки

Номер условия	Подшип-ник в точке	Крепление в точке		a, град	b, град	g, град	j, град
Номер условия	Подшип-ник в точке	ломанного стержня	невесомого стержня	a, град	Рис. 0–4	Рис. 5–9	j, град


	E	D	K
	К	B	D
	E	D	B
	K	K	B
	D	K	E
	E	B	K
	B	D	K
	K	D	E
	D	E	K
	B	K	D

Номер чертежа выбирается по последней цифре номера зачетки


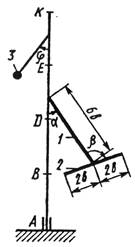
Рис. 0	Рис. 1	Рис. 2	Рис. 3

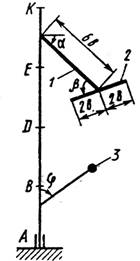
Рис. 4	Рис. 5	Рис. 6	Рис. 7

Рис. 8		Рис. 9

Массы элементов конструкции выбираются по последней цифре номера зачетки

Таблица № 2

Номер варианта
m2(кг)				5,5
т₃(кг)	3,5	2,5	4,5	5,5

12 Следующая ⇒