- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение задач. Посмотрите внимательно решение.
20.05.2020. Урок геометрии.
Учитель: Сидорова Н. И.
Урок 64. Решение задач по теме «Окружность»
| Цель | Создать условия для систематизации теоретического материала главы, подготовки к контрольной работе; совершенствовать навыки решения задач по теме «Окружность» | |
Решение задач. Посмотрите внимательно решение.
Задача 1.
Через точку А окружности проведены диаметр АС и две хорды АВ и AD так, что хорда АВ равна радиусу окружности, точка D делит полуокружность АС на две равные дуги. Найдите углы четырехугольника ABCD, если точки С и D лежат по разные стороны от диаметра АС.
Решение:
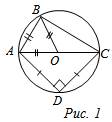
| 1) ÐABC = ÐADC = 90°, как вписанные углы, опирающиеся на диаметр. 2) ∆АОВ – равносторонний, так как АО = ВО как радиусы, а хорда АВ равна радиусу, тогда ÐBAO = 60°, ÐBCO = 30°. 3) Точка D делит полуокружность АС на две равные дуги AD и DC, поэтому хорды AD и DC равны, то есть ∆ADC – равнобедренный прямоугольный, поэтому ÐDAC = ÐDCA = 45°. |
4) ÐBAD = ÐBAC + ÐDAC = 60° + 45° = 105°.
5) ÐBCD = ÐBCO + ÐDCA = 30° + 45° = 75°.
Задача 2.
Основание равнобедренного треугольника равно 18 см, а высота, проведенная к нему, равна 12 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Решение:
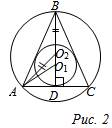
| ∆AO2D – прямоугольный, по теореме Пифагора 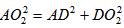 . Точка О2 – центр описанной окружности – лежит на биссектрисе, медиане, высоте, а значит, на серединном перпендикуляре, проведенном к основанию.
BD = 12 см, BO2 = R Þ DO2 = 12 – R, R2 = 92 + (12 – R)2.
R2 = 81 + 144 – 24R + R2, 24R = 225, R = 9,375.
|
Центр вписанной окружности также лежит на BD. АО1 – биссектриса ÐBAC, следовательно АВ : ВО1 = АD : DО1. По теореме Пифагора в ∆АВD: АВ2 = АD2 + ВD2 = 81 + 144 = 225, значит, АВ = 15 см. Так как ВО2 = R, то:
DO1 = BD – BO2 – О1О2 = 12 – 9,375 – О1О2
ВО1 = ВО2 + О1О2 = 9,375 + О1О2
15 ∙ (2,625 – О1О2) = 9 ∙ (9,375 + О1О2), О1О2 = –1, 875.
Так как О1О2 < 0 Þ О1 лежит между точками В и О2, тогда DO1 – O1O2 = 2,625 + 1,875 = 4,5 см
Домашнее задание:
Обратная связь