Симплексный метод решения задач линейного программирования

Симплексный метод решения задач линейного программирования

Данные метод состоит в целенаправленном переборе опорных решений задачи линейного программирования. Он позволяет за конечное число шагов расчёта либо найти оптимальное решение, либо установить его отсутствие.

Симплексные таблицы

Систему ограничений сведем к единичному базису:

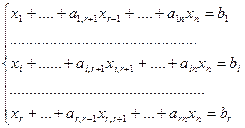
и линейную форму L – к виду

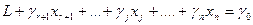В виде таблицы эти данные можно представить так:

Базисные перемен-ные	Свобод- ные члены	X₁	…	X_i	…	X_r	X_r+1	…	X_j	…	X_n
X₁	b₁		…		…		a_{1, r+1}	…	a_1i	…	a_1n
…	…	…	…	…	…	…	…	…	…	…	…
X_i	b_i		…		…		a_i_{, r+1}	…	a_i_,j	…	a_i_n
…	…	…	…	…	…	…	…	…	…	…	…
X_r	b_r		…		…		a_r_{, r+1}	…	a_r_,j	…	a_r_,n
L	γ₀		…		…		γ_r+₁	…	γ_j	…	γ_n

Равенство (**) будем называть приведённым (к свободным переменным) выражением для функции L, а коэффициенты γ_j - оценками (индексами) соответствующих свободных переменных x_j.

1) Выбирается разрешающий столбец a_p из условия: оценка γ_p<0 и хотя бы один элемент a_ip>0.

2) Выбирается q-я разрешающая строка из условия

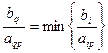для a_ip>0.

3) Производится пересчёт элементов разрешающей q-й строки по формуле

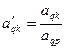(k=0, 1, …, n).

4) Вычисляются элементы всех остальных строк (при k ≠ p) по формуле

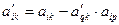(i=0,1, …, q-1, q+1, …, r).

Теорема. Если после выполнения очередной итерации:

1) найдется хотя бы одна отрицательная оценка и в каждом столбце с такой оценкой будет хотя бы один положительный элемент, т.е. γ_k<0 для некоторых k, и a_ik>0 для тех же k и некоторого i, то можно улучшить решение, выполнив следующую итерацию:

2) найдётся хотя бы одна отрицательная оценка, столбец которой не содержит положительных элементов, т.е.

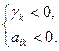
для какого-то k и всех i, то функция L не ограничена в области допустимых решений ( );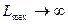

3) все оценки окажутся неотрицательными, т.е. 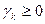для всех k, то достигнуто оптимальное решение.