Хелпикс

Главная

Контакты

Случайная статья



Системы однородных линейных уравнений



 Системы однородных линейных уравнений

первого порядка с постоянными коэффициентами

 

Для решения системы уравнений

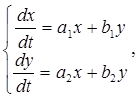                                                                               (1)

где x (t), y (t) – искомые функции, а1,2, b1,2 = const, нужно решить характери-стическое уравнение

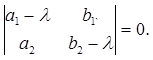                                                                         (2)

Если корни этого уравнения 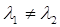 действительные, то решением системы (1) будут функции вида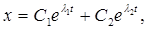 , причем произ-вольные постоянные С3 и С4 можно выразить через С1 и С2, подставив полу-ченные функции в систему.

Пример .Решить задачу Коши для системы 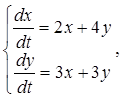 если х (0) = 2, у(0) = - 5 . Решение.

Составим характеристическое уравнение: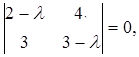

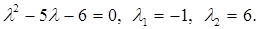 Следовательно,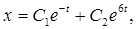 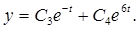 Тогда 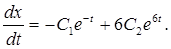 Подставим полученные выражения в первое уравнение системы:

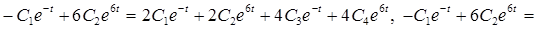
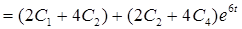, откуда

Итак, общее решение системы: 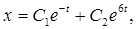 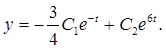При t = 0 получаем: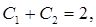 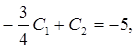 откуда С1 = 4, С2 = - 2, и частное решение системы: х = 4e-t – 2e6t, y = - 3e-t  - 2e6t.

При совпадении корней характеристического уравнения (2) решением системы (1) будут функци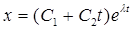и  и 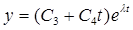, где λ – корень уравнения (2). Связь между С1, С2 и С3, С4 определяется аналогично предыдущему случаю.

Если корни характеристического уравнения – комплексно сопряженные числа α + βi и α – βi, решение системы (1) ищется в виде: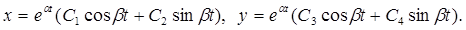

 

Воробьёва Анастасия

1.

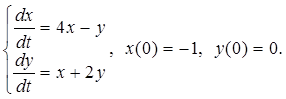
2.

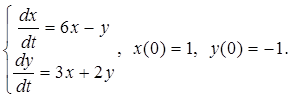
3.

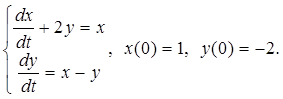
Загарий Анна

1.

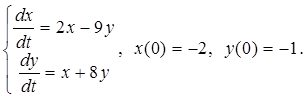
2.

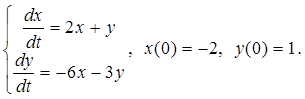
3.

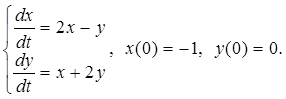
Зеновенков Андрей

1.

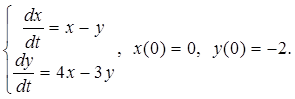
2.

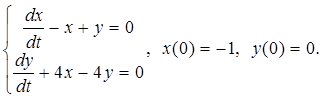
3.

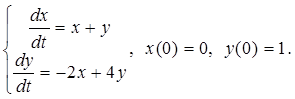
Петренко Александра

1.

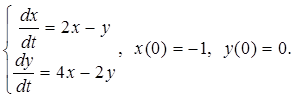
2.

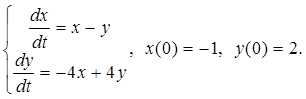
3.

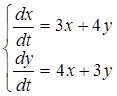
Труфанова Карина

1.

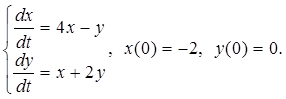
2.

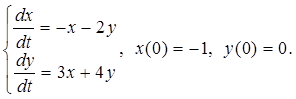
3.



  

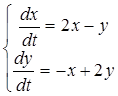
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.