ПРИМЕР ЗАДАНИЙ ПРОШЛЫХ ЛЕТ. Олимпиада первокурсников ТИУ 2016

26 октября олимпиада по математике среди первокурсников.

Открытие олимпиады состоится в аудитории 508 7 корпуса в 9-00.

Решение задач с 9-30 до 12-30 в аудиториях 508, 510, 512 и 526.

Дополнительная информация будет на сайте ТИУ после 16 октября.

ПРИМЕР ЗАДАНИЙ ПРОШЛЫХ ЛЕТ

Олимпиада первокурсников ТИУ 2016

1. Пусть матриц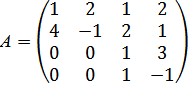а , а 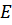– единичная матрица четвертого порядка. При каких значениях матрица 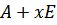имеет обратную?

2. На плоскости выбраны 4 точки, никакие три из которых не лежат на одной прямой. Докажите, что какие-то 3 точки образуют неостроугольный треугольник.

В ответ записать значение выражения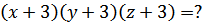

4. При каждом сравнить значения функций и .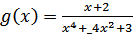

5. Найти определитель матрицы , если известно, что

6. Найти расстояние от точки А(0, 1) до параболы .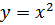

7. Найти и изобразить область определения функции

8. На клавиатуре калькулятора цифровые клавиши расположены так:

Доказать, что четырехзначное число, набираемое по ходу часовой стрелки или против нее из цифр, стоящих в углах любого прямоугольника, образованного цифровыми клавишами (например, 7777, 7887, 7964, 8965, 8932 и т.д.) делится на 11.