КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ

КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ

Кручение – вид сопротивления, при котором в поперечных сечениях бруса возникает только один внутренний силовой фактор – крутящий момент Т. Остальные силовые факторы (N, Qy, Qz, My, Mz) отсутствуют.

Вал – брус, работающий на кручение.

Принято внешние силовые факторы называть вращающими или скручивающими моментами и обозначать М; внутренние усилия – крутящим моментом

Т (от англ. torsion, torque)

В расчетах на прочность и жесткость при кручении знак крутящего момента значения не имеет, но для удобства построения эпюр принято правило:

Крутящий момент считают положительным, если при взгляде в торец отсеченной части бруса он стремится вращать сечение против хода часовой стрелки.

Положительный крутящий момент вызывает положительные касательные напряжения

5.1. ВНУТРЕННИЕ УСИЛИЯ ПРИ КРУЧЕНИИ

На основании метода сечений крутящий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме внешних скручивающих моментов, приложенных к брусу по одну сторону от рассматриваемого сечения.

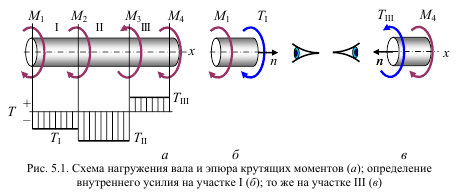
На рис. 5.1, б: ∑ M x = 0; T₁ + M₁ = 0; T₁ = −M₁.

На рис. 5.1, в: ∑ M x = 0; T_III – M₄ = 0; T_III = M4.

Эпюра крутящих моментов – график изменения крутящих моментов по длине бруса.

Во всех случаях эпюры внутренних усилий строят на осевой линии бруса.

Величину силового фактора откладывают по нормали к оси.

5.2. НАПРЯЖЕНИЯ ПРИ КРУЧЕНИИ

Теория брусьев, имеющих круглое сплошное или кольцевое поперечное сечение, основана на следующих положениях.

Поперечные сечения бруса плоские до деформации остаются плоскими и в деформированном состоянии – гипотеза твердых дисков (Бернулли).

Радиусы поперечных сечений не искривляются и сохраняют свою длину. Поперечные сечения остаются круглыми.

Расстояния между поперечными сечениями вдоль оси бруса не изменяются.

Для установления связи напряжений с внутренними усилиями рассмотрим несколько этапов решения задачи.

I. Условие равновесия – статическая сторона задачи (рис. 5.2, в).

τ·dA – элементарное усилие;

ρ·(τ·dA) – элементарный крутящий момент;

Т – равнодействующий момент касательных напряжений

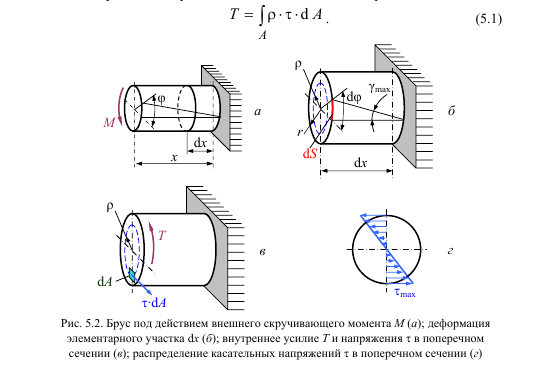
Для нахождения сдвигающих напряжений τ рассмотрим физическую

сторону задачи.

II. Физическая сторона задачи – закон Гука при сдвиге

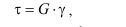(5.2)

связывающий касательные напряжения τ с деформацией сдвига γ. Деформацию сдвига γ найдем, рассмотрев геометрическую сторону задачи.

III. Деформационная (геометрическая) сторона задачи Левый торец бруса длиной х (рис. 5.2, а) под действием внешнего скручивающего момента М повернется на угол φ. В элементе длиной dx аналогичный угол dφ (рис. 5.2, б). Образующая цилиндра отклоняется от исходного положения на угол γ. На поверхности элемента радиусом r угол γ принимает максимальное значение

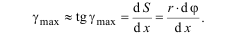
В цилиндре произвольного радиуса ρ внутри элемента угол γ:

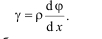(5.3)

Рассмотренные ранее этапы объединяет математическая сторона задачи.

Закон распределения касательных напряжений – линейный. В центре τ = 0,

так как ρ = 0, на периферии τ = τ_max, так как ρ_max= r (рис. 5.2, г).