Ответ: 2 детали по 3 кг и 3 детали по 8 кг.

Рассмотрим несколько олимпиадных заданий и задач ЕГЭ.

Пример 1. Докажите, что для любых натуральных чисел n и m существуют целые числа p и q, такие что НОД(n, m) = pn + qm.

Пример 2. Остаток от деления некоторого натурального числа n на 6 равен 4, остаток от деления n на 15 равен 7. Чему равен остаток от деления n на 30? (16)

Пример 3. Родительский комитет закупил на 750 рублей тетради по цене 35 рублей и ручки по цене 25 рублей. Сколько было куплено тетрадей и ручек, если ручек было куплено больше, чем тетрадей, а разница между количеством ручек и тетрадей наименьшая.

Пример 4. Строительная компания получила заказ на строительство 60 двухэтажных и 20 трехэтажных коттеджных домов. Каждая из 22 строительных бригад затрачивает на строительство 5 двухэтажных домов время, за которое она могла бы построить 3 трехэтажных. Сколько бригад следует выделить для строительства домов каждого типа, чтобы выполнить заказ за наименьшее время при условии, что все бригады приступят к работе одновременно и каждая из бригад будет занята строительством домов одного типа?

Пример 5. Красный карандаш стоит 18 рублей, синий — 14 рублей. Нужно купить карандаши, имея всего 499 рублей и соблюдая дополнительное условие: число синих карандашей не должно отличаться от числа красных карандашей больше чем на шесть.

а) Можно ли купить 30 карандашей?

б) Можно ли купить 33 карандаша?

в) Какое наибольшее число карандашей можно купить?

Всех их объединяет метод решения. Каждое из этих заданий приводит к решению

Уравнений в целых числах

Целью нашего занятия будет ознакомится с различными приемами и методами решения уравнений в целых числах и научиться решать их на практике.

1.Метод прямого перебора

Данный метод удобен, если коэффициенты уравнения невелики, а число решений конечно. Очень часто этот метод используется как часть других приемов.

Задача 1. Имеются детали массой 8 кг и 3 кг . Сколько необходимо взять тех и других деталей, чтобы получить груз 30 кг?

Решение:

Пусть х – количество деталей массой 3 кг, а у - количество деталей массой 8 кг.

Составим уравнение: 3х + 8у=30

Если х = 1, то 8у =27 , следовательно, у не является натуральным числом

Если х =2, то 8у =24 , следовательно, у =3

Если х = 3, то 8у =21 , следовательно, у не является натуральным числом

Если х = 4, то 8у =18 , следовательно, у не является натуральным числом

Если х =5, то 8у =15 , следовательно, у не является натуральным числом

Если х = 6, то 8у =12 , следовательно, у не является натуральным числом

Если х = 7, то 8у =9 , следовательно, у не является натуральным числом

Если х = 8, то 8·3+8>30 ,

Ответ: 2 детали по 3 кг и 3 детали по 8 кг.

2.Использование неравенств

Данный прием позволяет существенно сократить число рассматриваемых вариантов. Чаще всего используется в том случае, если возможно определить верхнюю/нижнюю границу перебора.

Задача 2. Решите в натуральных числах уравнение 3x + 6y = 21.

Решение.Для уменьшения перебора вариантов 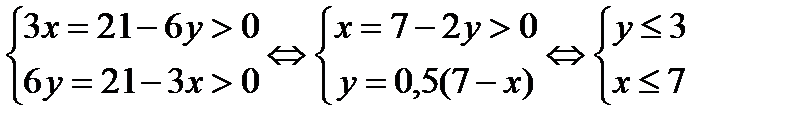рассмотрим неравенства

Проведем перебор по неизвестной у.

Если y = 1, то x = 5

Если y = 2, то x = 3

Если y = 3, то x = 1.

Ответ: (5;1), (3; 2)(;1;3).

3.Использование отношения делимости

Задача 3. Решить уравнение в целых числах 13x +16y = 300.

Решение. 13x +13y + 3y = 13· 23 +1,

3y −1 = 13(23 − x − y).

Отсюда следует, что разность 3y −1 делится на 13.

Если 3y −1 = 0, то у не является натуральным числом.

Если 3y −1 = 13, то у не является натуральным числом.

Если 3y −1 = 26, то y = 9 и x = 12.

Если 3y −1 = 39, то у не является натуральным числом.

Если 3y −1 = 52, то у не является натуральным числом

Если 3y −1 = 65, то y = 22, но16·22 = 352 > 300.

Ответ: (12;9)

4. Выделение целой части

Задача 4. Решить уравнение 8x + 5y = 39 .

Решение. Выразим у из уравнения и выделим целую часть:

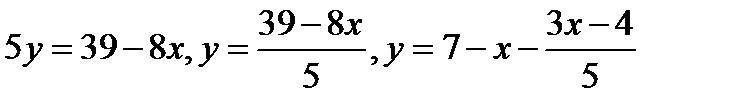
Отсюда следует, что разность 3x − 4 делится на 5.

Если 3x − 4 = 0, то х не является натуральным числом.

Если 3x − 4 = 5, то x = 3 и y = 3.

Если 3x − 4 = 10, то х не является натуральным числом.

Если 3x − 4 = 15, то х не является натуральным числом.

Если 3x − 4 = 20, то x = 8, но 8 8 = 64 > 39.

Ответ: (3; 3).

5. Метод остатков

Задача 5. Решите уравнение 3x − 4y = 1 в целых числах.

Решение.

Перепишем уравнение в виде 3x = 4y +1. Поскольку левая часть уравнения делится на 3, то должна делиться на 3 и правая часть. Рассмотрим три случая.

1) Если y = 3m, где m Z, то 4y +1 = 12m +1 не делится на 3.

2) Если y = 3m +1, то 4y +1 = 4(3m +1) +1 = 12m + 5 не делится на 3.

3) Если y = 3m + 2, то 4y +1 = 4(3m + 2) +1 = 12m + 9 делится на 3, поэтому 3x = 12m + 9,

x = 4m + 3.

Ответ: x = 4m + 3, y = 3m + 2, где m 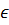Z.

6. Метод «спуска»

Задача 6. Решите в целых числах уравнение 5x − 7 y = 3.

Решение.Выразим из уравнения то неизвестное, коэффициент при котором

меньше по модулю:

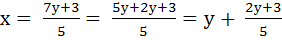Дробь 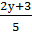должна быть равна целому числу.

Пусть 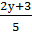, где z – целое число.

Тогда 2y + 3 = 5z. Из последнего уравнения выразим то неизвестное, коэффициент при котором меньше по модулю, и проделаем аналогичные преобразования:

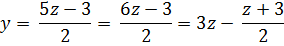
Дробь 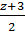должна быть целым числом.

Обозначим 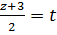, где t– целое число.

Отсюда z = 2t − 3. Последовательно возвращаемся к неизвестным х и у:

y = 3(2t − 3) − t = 5t − 9,

x = y + z = 5t − 9 + 2t − 3 = 7t −12.

Ответ: x = 7t – 12, y = 5t – 9, где t – целое число.

7.Метод последовательного уменьшения коэффициентов по модулю

Задача 7. Решить уравнение в целых числах 20х + 3у=10

Решение. Коэффициенты при переменных х и у – взаимно простые числа и свободный член - целое число. Коэффициент при х больше коэффициента при у. Представим его в виде суммы двух натуральных слагаемых так, чтобы первое слагаемое было наибольшим числом, кратным числу 3 (коэффициенту при у). Получим:

20х + 3у = 10

(18 +2) х +3у=10

18х +2х+3у=10

3(6х+у)+2х=10

Обозначим выражение 6х + у = k. (1)

Получим уравнение 3k+2x =10 с переменными k и х. Проведем аналогичные преобразования с полученным уравнением:

(2 + 1) k + 2 x =10

2(k + x) + k =10

Обозначим выражение k + х = n (2). Получим уравнение

2 n + k =10

k = 10 – 2n

Подставим в равенство (2) вместо k выражение 10 – 2n:

10 – 2n +x = n

x = 3n – 10

Мы получили одну из формул решений уравнения

20x – 3y = 10

Чтобы получить вторую формулу, подставим в равенство(1) вместо х

выражение +3n -10, а вместо k выражение 10-2n:

6(3n – 10)+y = 10 – 20n

y = 70 – 20n

Формулы х = 3n – 10; y = 70 – 20n при n = 0, ± 1, ±2; … дают все целочисленные решения уравнения/

8 . Использование формул

Задача 8. Найти целочисленные решения уравнения 13х = 6у - 19

Решение. Найдем одно целочисленное решение уравнения подбором: x₀ = - 1 , y₀ = 1 и выполним преобразования

13x = 6y – 16, 6y – 13x = 19,

Добавим и вычтем единицу

6(у – 1 + 1) – 13(х – 1 + 1) = 19, 6(у – 1) + 6 – 13(х + 1) + 13 = 19, тогда

из равенства 6(у – 1) – 13(х + 1) = 0 делаем вывод, что разность равна нулю только тогда, когда (у – 1) кратно 13 и (х + 1) кратно 6.

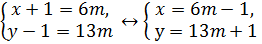
Ответ: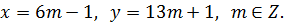

9. Использование конечных цепных дробей

Задача 9. Решите в целых числах уравнение 127x − 52y +1= 0

Решение.Преобразуем отношение коэффициентов при неизвестных. Прежде всего, выделим целую часть неправильной дроби .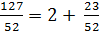

Правильную дробь 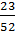заменим равной ей дробью .

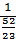Тогда получим

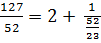
Проделаем такие же преобразования с полученной в знаменателе неправильной дробью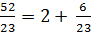

Теперь исходная дробь примет вид:

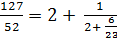Повторяя те же рассуждения для дроби 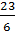получим 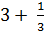. Тогда

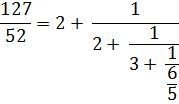
Выделяя целую часть неправильной дроби , придем к окончательному результату:

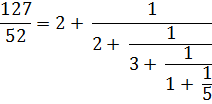
Мы получили выражение, которое называется конечной

цепной или непрерывной дробью.

Отбросив последнее звено этой цепной дроби –одну

пятую, превратим получающуюся при этом новую

цепную дробь в простую и вычтем ее из исходной дроби :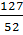

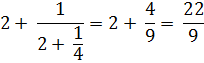
Итак,

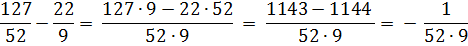
Приведем полученное выражение к общему знаменателю и

отбросив знаменатель, получим: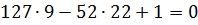

Из сопоставления полученного равенства с уравнением

127x − 52y +1= 0 следует, что x = 9 , y = 22 будет решением

этого уравнения, и согласно теореме все его решения будут

содержаться в формулах x = 9 + 52t , y = 22 +127t ,где 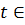Z.

Ответ: x = 9 + 52t , y = 22 + 127t , где t 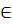Z.

Задания для самостоятельного решения

1) 20х + 12у = 2013;

2) 5х + 7у = 19;

3) 10х – 3у = 29.

Замечание: Для решения уравнения в целых коэффициентах достаточно хорошо освоить 2-3 способа по вашему выбору.

Решение приведенных выше примеров будет рассмотрено на следующем занятии. Также мы рассмотрим способы решения нелинейных уравнений вс целыми коэффициентами