Тема: Принятие управленческих решений в условиях полной информации. Математическое программирование

06-05/2020

Лекция

Тема: Принятие управленческих решений в условиях полной информации. Математическое программирование

управленческих решений (далее – УР)

Цель - дать представление о подходах к рациональному выбору решений в условиях неопределенности, нейтралитета и содействия, познакомить с фундаментальными понятиями и результатами теории статистических игр, а также помочь овладеть разнообразными методами решения задач теории статистических игр.

В результате освоения материала студент должен быть готов продемонстрировать следующие компетенции и уровень подготовки: В

· знание основных видов неопределенности, статистических критериев принятия решений в игре с природой (общетеоретический уровень);

· умение сделать выбор на основе эксперимента и в условиях содействия (уровень пользователя);

· навыки принятия статистических решений в условиях неопределенности, принятия решений в задачах о назначении (уровень проектировщика).

Игра с природой

Рассмотрим пример следующей задачи принятия решений.

ПРИМЕР Руководство предприятия должно принять решение: остановить работу конвейера и провести полную проверку его технического состояния или ограничиться текущей профилактикой без приостановки выпуска продукции? Эти решения отличаются затратами на проверку конвейера, ремонт, недополученной прибылью и т.п. Каждый из двух вариантов решения имеет свои плюсы и минусы.

Для принятия решения явно не хватает следующей количественной информации:

насколько вероятна вовремя не обнаруженная неисправность, которая может привести к капитальной поломке конвейера?

какова будет прибыль предприятия при различных вариантах сочетания: остановка и полная проверка конвейера – конвейер исправен;

остановка и полная проверка конвейера – реальная угроза серьезной неисправности и поломки;

текущая профилактика конвейера без приостановки выпуска продукции - конвейер исправен;

текущая профилактика конвейера без приостановки выпуска продукции – реальная угроза серьезной неисправности и поломки?

На эти вопросы руководитель предприятия заранее поручил ответить соответствующим специалистам.

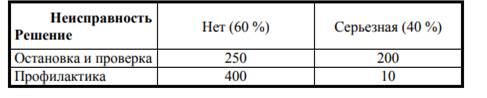
Перед началом заседания руководство получило от специалистов нужные для принятия решения количественные данные, сведенные в таблицу, отражающую месячную прибыль предприятия (тыс. руб.)

На заседании в процессе принятия решения началась дискуссия.

Рассмотрим ее ход и прокомментируем предлагаемые решения.

«Полагаю, надо получить максимум прибыли в самом плохом случае, – сказал бухгалтер. – Хуже всего будет, если оправдается риск серьезной неисправности конвейера. Прибыль предприятия в этом случае уменьшается при любом нашем решении. Останавливая конвейер, заработаем 200 тысяч, а ограничившись профилактикой – всего 10 тысяч. Надо временно остановить и провести ремонт конвейера».

Таким образом, бухгалтер предложил исходить из наихудшего случая - реальной угрозы серьезной неисправности и поломки конвейера.

В терминологии теории игр он рассматривал внешний для предприятия мир (техническое состояние конвейера) как противника, который всячески будет стараться уменьшить прибыль предприятия.

В условиях противоборства он предложил выбрать наиболее выгодный вариант решения – остановку и полную проверку конвейера. Этот пессимистический подход нам хорошо известен из теории антагонистических игр. В данном случае нет оснований считать внешний мир активным сознательным противником предприятия, тем более что вероятность неисправности равна 40 %.

«Нельзя быть таким пессимистом, - заявил технолог. Вероятность исправной работы конвейера равна 60 %. Надо быть оптимистами - исходить из того, что оборудование будет работать нормально. Тогда, останавливая конвейер, получим 250 тысяч в бюджет предприятия, а ограничившись профилактикой – 400 тысяч».

Подход технолога является прямо противоположным подходу бухгалтера. Он предлагает исходить из самого благоприятного стечения обстоятельств. Основание для такой позиции есть – вероятность исправной работы конвейера в полтора раза выше, чем вероятность неисправности. С точки зрения теории планирования это предложение можно было бы взять за основу, добавив возможности коррекции плана в случае возникновения неблагоприятных обстоятельств в процессе профилактики оборудования. Однако тогда необходимо расширять рамки дискуссии на заседании, рассмотрев решение о подготовке более гибкой производственной программы «двойного назначения». Оптимизм технолога не менее и не более оправдан, чем пессимизм бухгалтера: одни ЛПР предпочитают твердый доход, отказавшись от риска, другие – уверены, что им повезет, играя в лотерею.

полезность денег - равна логарифму имеющейся суммы.

«Бухгалтер и технолог обсуждают крайние ситуации, а надо подходить системно и всесторонне, учесть обе возможности, - начал свое выступление главный инженер, изучавший в вузе теорию вероятностей. - Рассмотрим сначала первый вариант - остановка и полная проверка конвейера. Мы получим 250 тысяч в 60 % случаев и 200 тысяч в 40 % случаев, значит, в среднем 250*0,6+200*0,4 = 150 + 80 = 230 тысяч. Для варианта текущей профилактики конвейера без приостановки выпуска продукции аналогичный расчет дает 400*0,6 + 10*0,4 = 240 + 4 = 244 тысячи, т.е. больше. Значит надо планировать текущую профилактику конвейера».

Это совсем другая позиция.

Главный инженер исходит из предположения, что придется много раз принимать решение о приостановке конвейера. Он рассчитывает средний доход, что выглядит вполне обоснованным, когда принятие подобного рода технико-экономических решений происходит чуть ли не каждый день. Тогда оценка математического ожидания прибыли вполне корректна. Однако на заседании речь идет об одном-единственном выборе. Поэтому 60 % и 40 % – это не вероятности как пределы частот. Это шансы исправной работы конвейера и неисправности. Иногда их полезно свести вместе в одном критерии.

«Главный инженер рассуждает так, как будто мы ежедневно принимаем решение о приостановке конвейера, а все данные в таблице сто лет не будут изменяться, - вступил в дискуссию экономист. - Необходимо принять решение только один раз и потом не жалеть об упущенных возможностях. Если мы решим остановить конвейер, а окажется, что он исправен, то упущенная прибыль составит 400 - 250 = 150 тысяч. Если мы ограничимся профилактикой, а серьезная неисправность приведет к поломке конвейера, то упущенная выгода составит 200 – 10 = 190 тысяч, т.е. будет больше. Значит, надо останавливать конвейер».

Экономист вводит в обсуждение новый критерий – «упущенная выгода». При этом средний доход, рассчитанный главным инженером, больше при текущей профилактике, а упущенная выгода, наоборот, меньше при остановке конвейера. Эти два критерия в данном случае противоречат друг другу.

Теория антагонистических игр базируется на предположении о том, что интересы игроков являются противоположными, и они действуют активно и разумно.

Представим теперь, что один из игроков является абстрактным лицом, например природой (окружающая среда), которая не имеет своих интересов и, следовательно, не ведет себя антагонистично по отношению к ЛПР.

Отсутствие противоборства со стороны природы не исключает для ЛПР необходимости рационального поведения. ЛПР зависит от состояний природы и должен их учитывать, принимая решение. Кроме того, у ЛПР имеется возможность путем эксперимента изучать природу.

Как в антагонистической игре, взаимодействие ЛПР и природы можно оценить матрицей выигрыша ЛПР E=(eij)m×n (если речь идет о потерях, то платежи в матрице будут отрицательными):

Информация о состоянии природы Fj (j = 1,…, n) всегда неполная. Возникает неустранимая неопределенность в принятии решения ЛПР, связанная со случайным характером многих явлений.

Принятие решения в этом случае связано с риском. Залог успешного принятия решения – правильное понимание сути задачи. Это особо актуально для слабо формализованных задач, к которым относится рациональный выбор в условиях неопределенности.

Принято различать статистическую и нечеткую неопределенность.

Статистическая неопределенность бывает частотной, объективной и субъективной. Различие между ними заключается в точности оценивания случайной величины. Природа нечеткой неопределенности также субъективна. Однако в отличие от статистической неопределенности, нечеткая неопределенность связана с ограниченным опытом ЛПР, с отношением ЛПР к окружающей среде на основе особенностей личности.

С другой стороны, Л. Заде в нечеткой логике указал на ограничения теории вероятности: она не позволяет отразить присущее ЛПР частичное восприятие природы: частичное знание, ограниченную точность, неполную истину, элементы веры и т.п.

Теория вероятности и математическая статистика моделирует лишь частичную определенность.

Пусть, например, некто по имени Франц имеет на три четверти немецкую, на четверть французскую кровь и считает себя немцем. Это утверждение можно оценить как истинное на 0,75. Но эта величина не имеет никакого отношения к вероятности! Вообще, теория вероятности ограничивается изучением стационарных или нестационарных, зависимых или независимых случайных процессов. При этом, например, сужение интервала случайной величины от [0, 10] до [2, 4] не приводит к уточнению вероятности, которая будет находиться на интервале [0, 1].

Теория игр с природой опирается на статистическую неопределенность. В зависимости от имеющейся информации о механизме выбора природой своих состояний различают случай полной и частичной статистической неопределенности. Различие между ними состоит в том, имеется или нет априорная информация о состояниях природы.

ПРИМЕР

При подготовке к сезону у фермера возникла проблема: «Что посадить – помидоры или картофель?». Помидоры, в отличие от картофеля, дают высокий урожай только жарким летом. Фермер подсчитал, что при жарком лете прибыль от помидор состовит 2 млн руб., а от картофеля – 1 млн руб. При холодном лете прибыль составит соответственно 0,5 и 1,5 млн руб.

Синоптики дали фермеру прогноз погоды на лето: вероятность жаркого лета равна 0,6, а холодного – 0,4.

В соответствии с условиями задачи, получаем следующую матрицу выигрыша:

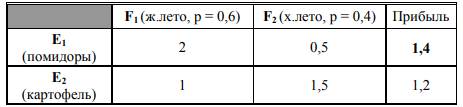
Используя априорную информацию, фермер определил выигрыш по среднему значению прибыли. Оптимальным будет решение Е1 – посадить помидоры. Если бы фермер решил минимизировать риск, то необходимо было бы определить упущенную выгоду:

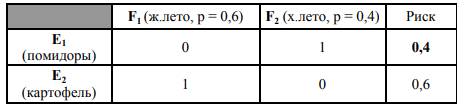
В этом случае оптимальным будет также решение Е1 – посадить помидоры. В теории статистических игр критерий «средний выигрыш» называется критерием Байеса–Лапласа, а в экономической теории – функцией полезности. Критерии выбора оптимального решения ЛПР в статистических играх, в отличие от антагонистических игр, могут быть различными.

Каждый, кто работает в области программной инженерии или занимается управлением этого процесса, рано или поздно начинает задавать себе непростые вопросы: почему при равных стартовых условиях один проект с треском проваливается, а другой приносит деньги и авторитет своим разработчикам? Представим себе, что разработка софта – это не инженерная наука (Майерс), не математика (Хоар), не искусство (Кнут), а игра (Коуберн) со своими правилами, ограниченными ресурсами и целями (поставить заказчику систему, создать основу для следующей системы и т.п.). Формулы, позволяющей всегда выигрывать в такой игре, пока не придумано. Однако есть некоторые приемы и принципы, которые могут быть полезны в той или иной ситуации. В самом деле, небезызвестный Линус Торвальдс не мог ведь сказать: «Выпустим приличную версию Linux - и по домам». Он в игре, игра ширится, развивается, пока не надоест своим участникам (похоже на игру с конструктором Lego).