Задание 1.. Задание 2.. Источники аргументации

Задание 1.

Используя таблицу причин, выявленных для проблемы, сформулированной в лабораторной работе 1, провести экспертную оценку значимости причин (оценку их весовых коффициентов) методом парных сравнений.

При парном сравнении необходимо в каждой из пар выявить более значимый объект или установить их равенство. Парное сравнение можно проводить при большом числе объектов, а также в тех случаях, когда различие между объектами столь незначительно, что практически невыполнимо их простое ранжирование.
При использовании метода чаще всего составляется матрица размером n_xn,

где

n – количество сравниваемых объектов.

Количество составленных матриц равно m – количеству экспертов

			---	j	---	n
	a₁₁	a₁₂	---	a_1j	---	a_1n
	a₂₁	a₂₂	---	a_2j	---	a_2n
---	---	---	---	---_j	---	---
i	a_i1	a_i2	---	a_ij	---	a_in
---	---	---	---	---	---	---
n	a_n1	a_n2	---	a_nj	---	a_nn

При сравнении объектов матрица заполняется элементами a_ij следующим образом (может быть предложена и иная схема заполнения):

2, если объект i предпочтительнее объекта j (i > j),
1, если установлено равенство объектов (i = j),
0, если объект j предпочтительнее объекта i (i < j).

1. Для выполнения экспертной оценки каждому эксперту составить матрицу парных сравнений причин возникновения проблемы. В качестве экспертов выступают члены рабочей группы, выполнявшие оценку проблемы с помощью метода " 7 инструментов качества".

Пример

Эксперт 1
причины




Эксперт 2
причины

2. На основании значений полученных матриц составить матрицу средних значений. Элемент матрицы равен:

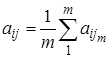
Пример

Матрица средних значений

			1.5
			1.5
	0.5	0.5

3. Для каждой i-й строки определить суммы частот предпочтений экспертов

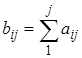
Матрица средних значений
				b
			1.5	2.5
			1.5	3.5
	0.5	0.5

4. Определить сумму всех частот строк b₀ по формуле:

Матрица средних значений
					b
			1.5		2.5
			1.5		3.5
	0.5	0.5

				b₀=12

5. Доля каждой причины составляет

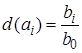
Матрица средних значений
					b	d(a_i)
			1.5		2.5	20.8%
			1.5		3.5	29.1%
	0.5	0.5				17%
						33%
				b₀=12

6. Можно присвоить каждой причине весовой коэффициент в соответствии с ее долей

Матрица средних значений
					b	d(a_i)	вес
			1.5		2.5	20.8%	0.2
			1.5		3.5	29.1%	0.3
	0.5	0.5				17%	0.17
						33%	0.33
				b₀=12

Задание 2.

Используя таблицу причин, выявленных для проблемы, сформулированной в лабораторной работе 1, провести их экспертную оценку методом простого ранжирования.

Пример

1. Составить матрицу для экспертной оценки, занести в нее все выявленные причины и представить экспертам для заполнения. Каждого эксперта просят расположить признаки в порядке предпочтения. Цифрой один обозначается наиболее важный признак, цифрой два – следующий за ним по важности и т.д. полученные данные сводятся в следующую таблицу.

Матрица экспертной оценки
Причина\эксперт

2. Определить суммарный ранг S_i i-го признака:

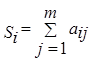
где

m – общее количество экспертов;

n – количество причин/критериев;

j – номер эксперта; i = 1,…, m;

i– номер признака, j = 1,2,…, n.

Матрица экспертной оценки
Причина\эксперт					S_i

3. Определить средний ранг, среднее статистическое значение S_i i-го признака

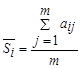
4. Определить средний ранг совокупности признаков :

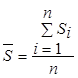
	Матрица экспертной оценки
Причина\эксперт		S_i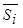
			1,25
			3,25
			2,25
			3,25

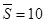
5. Вычисляется отклонение d_j среднего ранга i-го признака от среднего ранга совокупности (дисперсия):

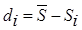
	Матрица экспертной оценки
Причина\эксперт		S_i		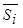d_i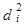
			1,25
			3,25	-3
			2,25
			3,25	-3

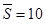
Для того чтобы можно было сказать, случайно ли распределение рангов или имеется согласованность в мнениях экспертов, производится вычисление коэффициента конкордации K, введенного М. Кендаллом.

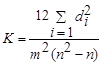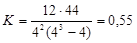
Коэффициент K может принимать значения в пределах от 0 до 1. При полной согласованности мнений экспертов коэффициент конкордации равен единице при полном разногласии – нулю. Наиболее реальным является случай частичной согласованности мнений экспертов.

По мере увеличения согласованности мнений экспертов коэффициент конкордации возрастает и в пределе стремится к единице. Однако даже если он равен или близок к нулю, не всегда имеет место полное разногласие. Среди экспертов могут быть группы с хорошо согласованными мнениями, но мнения эти – противоположны и в общей массе нейтрализуют друг друга.

Определить в качестве показателя компетентности эксперта коэффициент:

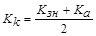где

K_к – коэффициент компетентности эксперта;

K_зн – коэффициент степени знакомства эксперта с обсуждаемой проблемой;

K_a – коэффициент аргументированности.

Коэффициент степени знакомства с направлением исследований определяется путем самооценки эксперта по десятибалльной шкале. Значения баллов для самооценки следующие:

0 – эксперт не знаком с вопросом;

1,2,3 – эксперт плохо знаком с вопросом, но вопрос входит в сферу его интересов;

4,5,6 – эксперт удовлетворительно знаком с вопросом, не принимает непосредственного участия в практическом решении вопроса;

7,8,9 – эксперт хорошо знаком с вопросом, участвует в практическом решении вопроса;

10 – вопрос входит в круг узкой специализации эксперта.

Эксперту предлагается самому оценить степень своего знакомства с вопросом и подчеркнуть соответствующий балл. Затем этот балл умножается на 0,1, и получается нужный коэффициент .

Коэффициент аргументированности учитывает структуру аргументов, послуживших эксперту основанием для определенной оценки. Коэффициент аргументированности предлагается определить в соответствии с Таблицей 1 путем суммирования значений, отмеченных экспертом в клетках этой таблицы.

Определив коэффициент компетентности, умножают на него значение оценок экспертов.

Таблица 1 – Значения коэффициента аргументированности

Источники аргументации

⇐ Предыдущая 123 Следующая ⇒