Контрольная работа (ТЕСТ). Производная. Применение производной к исследованию функции»

Контрольная работа (ТЕСТ)

«Производная. Применение производной к исследованию функции»

Часть 1.

1.	Производная функции – это … 1) расстояние; 2) мгновенная скорость; 3) ускорение.	1 б.
2.	Как называется операция нахождения производной? 1) потенцирование; 2) интегрирование; 3) дифференцирование.	1 б.
3.	Точки, в которых производная равна нулю, называются: 1) стационарными; 2) критическими; 3) точками экстремума.	1 б.
4.	Если две дифференцируемые функции отличаются на постоянное слагаемое, то: 1) их производные равны; 2) их производные различаются на разность постоянных слагаемых; 3) вопрос о различии их производных установить не удаётся.	2 б.
5.	Если на интервале функция возрастает, то значение производной на этом интервале: 1) равно нулю; 2) больше нуля; 3) меньше нуля.	2 б.
6.	Дифференцируемая функция может иметь экстремум в тех точках, где: 1) производная не существует; 2) производная равна нулю; 3) производная равна нулю и не существует.	2 б.
7.	Если график производной расположен выше оси Ох на интервале, то функция: 1) возрастает на этом интервале; 2) убывает на этом интервале; 3) постоянна на этом интервале.	2 б.
8.	Если график производной пересекает ось Ох в точке х₀, располагаясь сначала ниже, потом выше оси Ох, то х₀ для функции является: 1) стационарной точкой; 2) точкой максимума; 3) точкой минимума.	2 б.
Итого		13 б.

Часть 2

1.	Производная функции у = 0,75х⁴ – 2 cosx равна: 1) y = 3x³ + 2 cosx; 2) y = 3x³ – 2sinx; 3) y = 3x³ - 2 cosx; 4) y = 3x³ + 2sinx.	1 б.
2.	Производная функции у = 2х – х² + 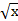в точке х₀ = 9 равна: 1) 27 ; 2) – 8 ; 3) - 27 ; 4) - 9 .	1 б.
3.	Решите уравнение у^/(х) = 0, если у(х) = 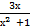: 1) 0; 2) 3; 3) корней нет; 4) 1; -1.	2 б.
4.	Материальная точка движется по закону S(t) = 3t + 7 + 0,5t², где t – время движения в секундах. Через какое время после начала движения скорость тела окажется равной 15 м/с? 1) 18; 2) 15; 3) 12; 4) 21.	2 б.
5.	Прямая у = - 4х + 11 является касательной к графику функции у = х² + 6 х + 2. Найдите абсциссу точки касания: 1) 2; 2) 5; 3) – 2; 4) -5.	2 б.
6.	На рисунке изображены график функции у = f(x) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции f(x) в точке х₀: 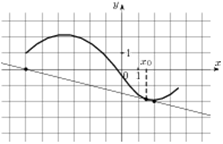1) 4; 2) -0,25; 3) 0,25; 4) – 4.	2 б.
7.	Дан график функции у = f(x). Сравните значения производной в точках х = - 5 и х = 5 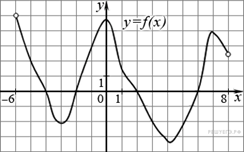1) f^/(-5) и f^/(5) не существует; 2) f^/(-5) = f^/(5); 3) f^/(-5) <f^/(5); 4) f^/(-5) >f^/(5).	2 б.
8.	На рисунке изображён график производной функции, определённой на интервале (-7; 4). Определите количество промежутков возрастания функции: 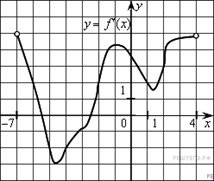1) 1; 2) 2; 3) 3; 4) 0.	2 б.
9.	На рисунке изображён график функции у = f(x), определённой на интервале (-7; 10). Найдите сумму точек экстремума функции на отрезке [- 4; 8]. 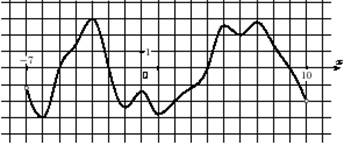1) 7; 2) 12; 3) 15; 4) 18.	2 б.
10.	На рисунке изображён график производной функции у = f^\(x), определённой на интервале (-8; 6). В какой точке отрезка [- 5; - 1] функция у = f(x) принимает наибольшее значение? 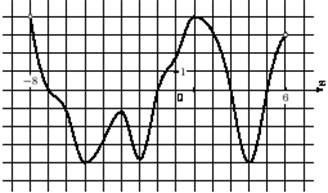1) -1; 2) -3; 3) -5; 4) -2	2 б.
11.	Найдите наименьшее и наибольшее значения функции f(x) = х^2/3(х - 2) на отрезке [-8; -1]: 1) -3 и 40; 2) -3 и - 40; 3) 40 и 3; 4) – 38 и -2.	3 б.
12.	Найти точки экстремума функции у= - 0,2 х - 5х^-1 и определить их характер: 1) 5 – максимум, - 5 – минимум; 2) -3 – максимум, 3 – минимум; 3) нет точек экстремума; 4) -5 – максимум, 5 – минимум	3 б.
Итого		24 б.

Оценивание.

Для оценивания результатов выполнения работы применяются отметки «2», «3», «4», или «5». Полное правильное выполнение всей работы – 37 б.

Отметка «3» выставляется, если набрано от 5 до 7 балловиз части I и от 5 до 9 балловиз части II.

Отметка «4» выставляется, если набрано от 8 до 10 балловиз части Iиот 10 до 15 балловиз части II;

Для получения отметки «5» необходимо набрать от 11 до 13 балловиз части I и от 16 до 24 баллов части II.