
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Принцип суперпозиции электростатических полей. Напряженность электрического поля на оси заряженного кольца
3.1.3. Принцип суперпозиции электростатических полей. Напряженность электрического поля на оси заряженного кольца
Для расчета 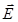 поля, созданного системой зарядов или макроскопическим заряженным телом, используют принцип суперпозиции: вектор напряженности
поля, созданного системой зарядов или макроскопическим заряженным телом, используют принцип суперпозиции: вектор напряженности 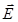 электрического поля, созданного несколькими зарядами, равен векторной сумме напряженностей полей, созданных каждым зарядом в отдельности (
электрического поля, созданного несколькими зарядами, равен векторной сумме напряженностей полей, созданных каждым зарядом в отдельности ( 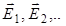 ) [3].
) [3].
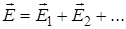 (3.8)
(3.8)
Для расчета напряженности электрического поля макроскопического заряженного тела в какой-либо точке A (рис. 3.3, а) необходимо разбить тело на бесконечно малые объемы, которые можно рассматривать как точечные заряды 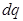 ). Затем по формуле (3.7) в точке А найти вектора
). Затем по формуле (3.7) в точке А найти вектора 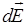 от этих зарядов и просуммировать их, т.е. взять интеграл по всему объему V тела
от этих зарядов и просуммировать их, т.е. взять интеграл по всему объему V тела
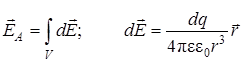 . (3.9)
. (3.9)
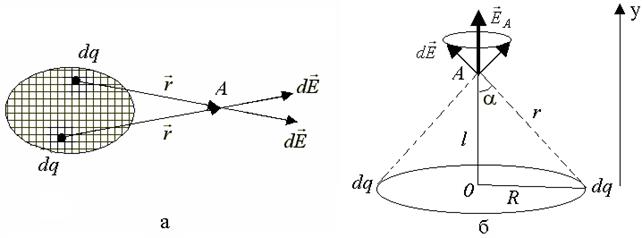
Рис. 3.3
Приведем пример расчета напряженности электростатического поля на оси равномерно заряженного кольца. Пусть равномерно заряженное по длине кольцо радиусом R несет заряд q. Найдем направление и модуль вектора 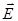 поля кольца в точке А, расположенной на оси кольца на расстоянии l от его центра (рис. 3.3, б). Для этого разбиваем кольцо на малые участки – точечные заряды dq, определяем направление векторов
поля кольца в точке А, расположенной на оси кольца на расстоянии l от его центра (рис. 3.3, б). Для этого разбиваем кольцо на малые участки – точечные заряды dq, определяем направление векторов 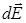 от всех зарядов dq в точке А и используем для расчета
от всех зарядов dq в точке А и используем для расчета 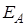 формулу (3.9). Из симметрии задачи видно, что все вектора
формулу (3.9). Из симметрии задачи видно, что все вектора 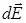 образуют конус векторов с углом a при его вершине и суммарный вектор
образуют конус векторов с углом a при его вершине и суммарный вектор 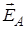 будет направлен вдоль оси, вверх [3].
будет направлен вдоль оси, вверх [3].
Тогда
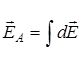 ;
;
Оу: 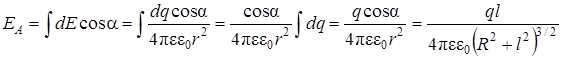 ;
;
где учтено, что
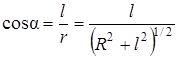 .
.
Таким образом, напряженность электрического поля в точке А, находящейся на оси заряженного кольца (рис. 3.3) вычисляется по формуле
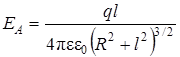 ; (3.10)
; (3.10)
Проанализируем полученное выражение. При l = 0, напряженность электростатического поля в центре кольца (точка О), равна
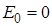 . (3.11)
. (3.11)
При l >>R кольцо можно рассматривать как материальную точку, следовательно напряженность электрического поля кольца рассчитывается по формуле (3.7) напряженности поля точечного заряда
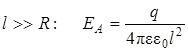 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|