Практическая работа №63. Теория.

Практическая работа №63

Тема Рациональные и иррациональные уравнения.

Цель: Повторение и систематизация знаний.

Теория.

Опр.

Уравнения, в которых неизвестная содержится в знаменателе дроби, называются рациональными.

Рациональные уравнения решают следующим образом, надо:

1) найти общий знаменатель дробей, входящих в уравнение;

2) заменить данное уравнение целым, умножив обе части на общий знаменатель;

3) решить получившееся уравнение;

4) исключить из него те корни, которые обращают в нуль общий знаменатель

Пример

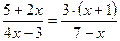
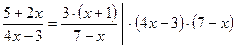
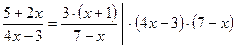
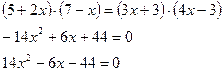
Проверка:

х= 2 4 · 2 – 3 = 5 ≠ 0 7 – 2 = 5 ≠ 0

х = - 5,5 4 · ( - 5,5) – 3 = - 25 ≠ 0 7 – ( - 5,5 ) = 7 + 5,5 = 12,5

Ответ:

Опр.

Уравнения, в которых переменная находится под знаком корня, называются иррациональными.

Для решения иррационального уравнения надо левую и правую части уравнения возвести в п-ую степень, равную показателю корня

Пример

1. Решение уравнения 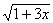= 1 – х методом возведения в квадрат обеих частей уравнения.
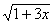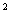( ) = (1 – х) ;

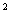1+ 3х = x² – 2x + 1;

x²– 5x = 0.
Решив это уравнение, находим корни .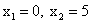

Проверка: если x = 0, то 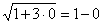, 1 = 1 – верно;
если х = 5, то 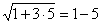, 4 = 4 – неверно.
Ответ: х = 0.

Литература:

1. Ш.А.Алимов «Алгебра и начала анализа» 10-11 кл. , стр. 58 - 60