
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа № 34.. Теория
Практическая работа № 34.
Тема: Задачи на отыскание наибольших и наименьших величин.
Цель: Применение знаний при решении задач.
Теория
На практике часто приходится решать задачи на нахождение наибольшего или наименьшего значения функции на отрезке.
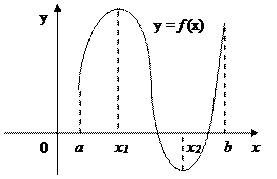
Наибольшее f(b), наименьшее f(x2)
x1, x2 – стационарные точки
Для нахождения наибольшего и наименьшего значений функции на отрезке [a; b] нужно:
1) найти значение функции на концах отрезка, т.е . f(a) и f( b) ;
2) найти её значения в тех критических точках, которые принадлежат интервалу (a;b)
3) из найденных значений выбрать наибольшее и наименьшее.
Замечание: Если на (a, b) нет стационарных точек, то наибольшее и наименьшее значения функция принимает на концах отрезка [a; b].
Пример:

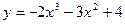 на [-2; 1]
на [-2; 1]
1) 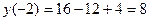
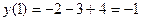
2) 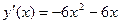
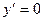 при
при 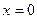 и
и 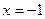
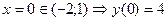
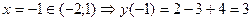
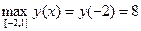
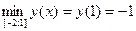
Для нахождения наибольшего и наименьшего значений функции на интервале ( a ; b ) , нужно:
Если функция дифференцируема на интервале ( a ; b ) и имеет только одну стационарную точку х0: это либо точку максимума, либо точку минимума, тогда
если х0 - точка максимума, то функция в этой точке принимает наибольшее значение;
если х0 - точка минимума, то функция в этой точке принимает наименьшее значение;
Задача
Число 36 записать в виде произведения 2-х положительных чисел, сумма которых наименьшая.
Решение
Пусть первый множитель равен х, тогда второй множитель равен 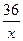 .
.
Сумма этих чисел равна 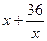 . По условию задачи х – положительное число. Таким образом задача свелась к нахождению такого значения х, при котором функция
. По условию задачи х – положительное число. Таким образом задача свелась к нахождению такого значения х, при котором функция 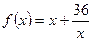 принимает наименьшее значение на интервале х > 0.
принимает наименьшее значение на интервале х > 0.
Найдём производную : 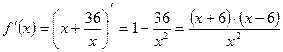
Стационарные точки: х1 = 6 и х2 = - 6. На интервале х > 0 есть только одна стационарная точка х= 6.
При переходе через точку х = 6 производная меняет знак с « - » на « + » , и поэтому точка х = 6 – точка минимума. Следовательно, наименьшее значение на интервале х > 0 функция 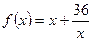 принимает в точке х = 6 . это значение
принимает в точке х = 6 . это значение 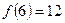
Ответ: 36 = 6 · 6
Пример
1) 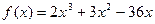 на [-4; 3]
на [-4; 3]
1) 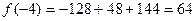
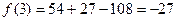
2) 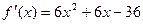
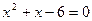
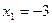
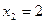 - Î (-4; 3)
- Î (-4; 3)
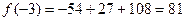
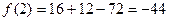
Ответ: 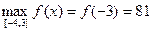
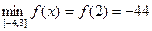
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|