
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Т а б л и ц а 11.1
Л а б о р а т о р н а я р а б о т а № 2
ИССЛЕДОВАНИЕ СЛОЖНОЙ РЕЗИСТИВНОЙ ЦЕПИ
2.1.Цель работы
1. Изучение методов расчета схем сложных электрических цепей.
2. Теоретическая и экспериментальная проверка принципа наложения в линейной цепи.
3. Теоретическая и экспериментальная проверка баланса токов в узлах цепи согласно 1-му закону Кирхгофа и баланса напряжений в контурах согласно 2-му закону Кирхгофа.
4. Теоретическая и экспериментальная проверка баланса мощностей в сложной цепи.
2.2. Исходные данные
Заданы:
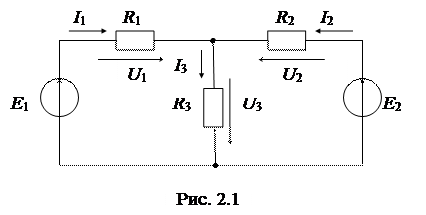
1. Эквивалентная схема исследуемой сложной цепи (рис. 2.1).
2. Параметры элементов схемы (табл. 2.1).
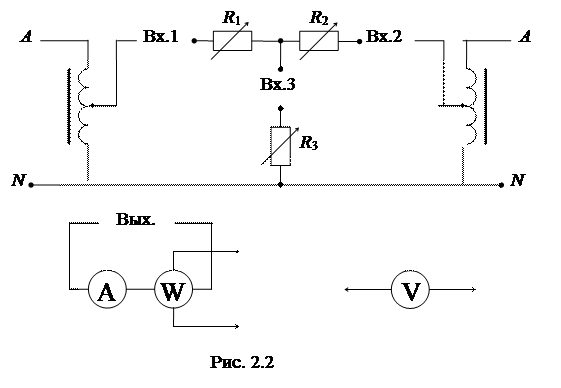
3. Рабочая схема исследуемой цепи и схемы включения измерительных приборов (рис. 2.2).
Т а б л и ц а 2.1
| Вариант | ||||||||||
| E1, В | ||||||||||
| E2, В | ||||||||||
| R1, Ом | ||||||||||
| R2, Ом | ||||||||||
| R3, Ом |
2.3. Теоретические сведения и методические указания
Электрическое состояние любой сложной схемы (цепи) определяется системой уравнений, составленных для нее по 1-му и 2-му законам Кирхгофа.
1-ый закон Кирхгофа: алгебраическая сумма токов в узле схемы (цепи) равна нулю, или åI=0.
2-ой закон Кирхгофа: алгебраическая сумма падений напряжений в замкнутом контуре схемы (цепи) равна алгебраической сумме ЭДС, или åU=åE.
Принцип наложения гласит: ток в любой ветви (напряжение на любом элементе) сложной схемы с несколькими источниками энергии равен алгебраической сумме частичных токов (напряжений), возникающих в этой ветви (на этом элементе) от независимого действия каждого источника энергии.
Для любой сложной схемы в соответствии с законом сохранения энергии должен выполняться баланс (равенство) между суммой мощностей источников и суммой мощностей приемников энергии: SРист= SРпр.
Расчет частичных токов и напряжений от независимого действия каждого источника энергии рекомендуется выполнять методом свертки схемы. Расчет токов в схеме с двумя источниками ЭДС следует выполнить одним из методов расчета сложных схем по выбору (метод законов Кирхгофа, метод контурных токов, метод двух узлов), а метод наложения использовать для проверки.
Для измерения токов и мощностей в нескольких ветвях цепи применяется коммутатор токовых цепей, позволяющий включать приборы (амперметр и ваттметр) поочередно в любую ветвь цепи.
2.4. Расчетная часть
1. Выполнить расчет схемы методом преобразования и определить частичные токи в ветвях схемы, напряжения на отдельных элементах и мощности источника энергии и отдельных приемников от независимого действия только одного источника ЭДС Е1 (Е2 = 0). Результаты расчета записать в табл. 2.2, 2.3.
2. Выполнить аналогичный п. 1 расчет схемы от независимого действия только одного источника ЭДС Е2 (Е1= 0). Результаты расчета записать в табл. 2.2, 2.3.
3. Выполнить полный расчет схемы при совместном действии всех источников энергии одним из методов расчета сложных схем по выбору (метод законов Кирхгофа, метод контурных токов, метод двух узлов). Определить токи в ветвях схемы, напряжения на отдельных элементах и мощности отдельных источников и приемников энергии. Результаты расчета записать в табл. 2.2, 2.3.
Т а б л и ц а 2.2
| Величины | E1, В | E2, В | I1, А | I2, А | I3, А | U1, В | U2, В | U3, В |
| Вычис. | ||||||||
| Измер. | ||||||||
| Вычис. | ||||||||
| Измер. | ||||||||
| Вычис. | ||||||||
| Измер. |
Т а б л и ц а 2.3
| Величины | E1, В | E2, В | РE1, Вт | РE2, Вт | Р1, Вт | Р2, Вт | Р3, Вт | SРИ, Вт | SРН, Вт |
| Вычис. | |||||||||
| Измер. | |||||||||
| Вычис. | |||||||||
| Измер. | |||||||||
| Вычис. | |||||||||
| Измер. |
2.5. Экспериментальная часть
1. Собрать электрическую цепь согласно рабочей схеме рис. 2.2. Установить заданные параметры сопротивлений резисторов. Включить источники энергии (ЭДС).
2. Установить напряжение на зажимах 1-го источника U = Е1, а на зажимах 2-го источника U = 0. Измерить частичные токи в ветвях, напряжения на отдельных участках, а также мощности источников и приемников от действия источника ЭДС Е1. Результаты измерений внести в табл. 2.2 ,2.3.
3. Установить напряжение на зажимах 2-го источника U = Е2, а на зажимах 1-го источника U = 0. Измерить частичные токи в ветвях , напряжения на отдельных участках, а также мощности источников и приемников от действия источника ЭДС Е2. Результаты измерений внести в табл. 2.2, 2.3.
4. Установить напряжение на зажимах 1-го источника U = Е1, а на зажимах 2-го источника U = Е2. Измерить токи в ветвях, напряжения на отдельных участках, а также мощности источников и приёмников от совместного действия обоих источников ЭДС Е1 и Е2. Результаты измерений внести в табл. 2.2, 2.3
2.6. Анализ результатов работы
1. Для каждой расчетной схемы проверить баланс токов в узле в соответствии с 1-м законом Кирхгофа ( SI = 0), баланс напряжений и ЭДС в контурах в соответствии со 2-м законом Кирхгофа ( SU = SE) и баланс мощностей источников и приемников энергии (SРист= SРпр). Проверить выполнение этих балансов для экспериментальных результатов измерений.
2. Проверить выполнение принципа наложения как для расчетных, так и для экспериментальных результатов.
3. Сопоставить результаты измерений с соответствующими данными расчета, в случае их существенного различия установить возможные причины.
2.7. Содержание отчета
Отчет по данной лабораторной работе должен содержать:
1) титульный лист по стандартной форме;
2) цель работы;
3) исходные данные (схему исследуемой цепи и параметры ее элементов);
4) таблицы с результатами вычислений и измерений;
5) основные расчетные формулы и уравнения;
6) уравнения баланса токов, напряжений и мощностей;
7) выводы и заключение о степени соответствия расчетных и экспериментальных результатов.
Контрольные вопросы
1. Как формулируется принцип наложения? Почему принцип наложения неприменим для мощностей?
2. Как составить систему уравнений для расчета токов в сложной схеме по законам Кирхгофа?
3. Как составить систему уравнений для расчета токов в сложной схеме по методу контурных токов?
4. Как составить систему уравнений для расчета токов в сложной схеме по методу узловых потенциалов? по методу двух узлов?
5. Что такое баланс мощностей для схемы и как его составить?
 Л а б о р а т о р н а я р а б о т а №4
Л а б о р а т о р н а я р а б о т а №4
ИССЛЕДОВАНИЕ ПРОСТЫХ ЦЕПЕЙ ПЕРЕМЕННОГО
СИНУСОИДАЛЬНОГО ТОКА
4.1. Цель работы
1. Анализ соотношений между напряжениями и токами и углов сдвига фаз между ними в простых цепях переменного синусоидального тока с последовательным или параллельным соединением резисторов, конденсаторов и катушек.
2. Изучение методов построения векторных диаграмм токов и напряжений для различных схем.
4.2. Исходные данные
Заданы:
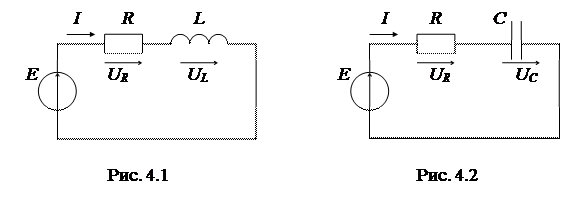
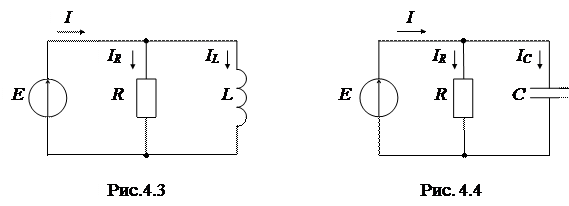
1. Эквивалентные схемы исследуемых цепей (рис. 4.1, 4.2, 4.3, 4.4).
2. Параметры элементов схем (табл. 4.1).
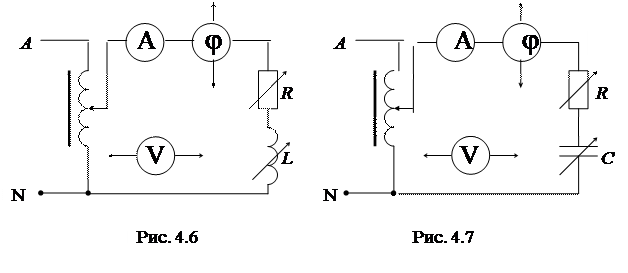
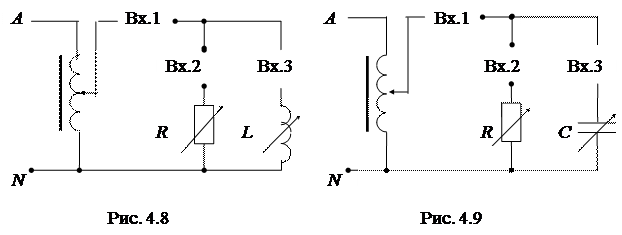
3. Рабочие схемы исследуемых цепей и схемы включения измерительных приборов (рис 4.5, 4.6, 4.7, 4.8).
 |
Т а б л и ц а 4.1.
| Вариант | ||||||||||
| U, В | ||||||||||
| R, Ом | ||||||||||
| XL , Ом | ||||||||||
| XC , Ом |
4.3. Теоретические сведения и методические указания
В линейных цепях переменного тока все режимные функции (токи, напряжения) изменяются во времени по синусоидальному закону: i(t)=Im×sin(wt+a), u(t)=Um×sin(wt+b). При расчете таких цепей синусоидальные функции времени заменяют векторами или комплексными числами и расчет выполняют соответственно в векторной или комплексной форме.
Алгоритм расчета схемы с последовательным соединением элементов R, L, C в векторной форме:
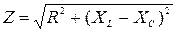 - полное сопротивление схемы [Ом], где
- полное сопротивление схемы [Ом], где
XL=wL, XC=1/wC - реактивные сопротивления катушки и конденсатора;
w = 2pf = 314- угловая частота [c-1], f =50-циклическая частота [Гц]; 
I = E/Z - ток в схеме [A];
UR=I ·R, UX= I ·X -напряжения на отдельных элементах [B];
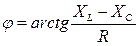 -угол сдвига фаз между напряжением и током [о].
-угол сдвига фаз между напряжением и током [о].
Алгоритм расчета той же схемы в комплексной форме:
Z= R+j(XL - XC)=Zejj - комплексное сопротивление схемы [Ом];
I = E / Z - комплексный ток в схеме [A];
UR=I ·R, UX=I · jX -напряжения на отдельных элементах [B].
Алгоритм расчета схемы с параллельным соединением элементов R, L, C в векторной форме:
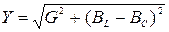 - полная проводимость схемы [См], где
- полная проводимость схемы [См], где
BL= 1/XL, BC=1/ XC - реактивные проводимости катушки и конденсатора;
I = E·Y - ток в схеме [A];
IR=E·G, IB=E·B -токи в отдельных элементах [А];
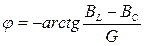 -угол сдвига фаз между напряжением и током .
-угол сдвига фаз между напряжением и током .
Алгоритм расчета той же схемы в комплексной форме:
Y= G -j(BL - BC)=Ye -jj - комплексная проводимость схемы [См];
I = E·Y - комплексный ток в схеме [A];
IR=E·G, IB=E· jB -токи в отдельных элементах [А].
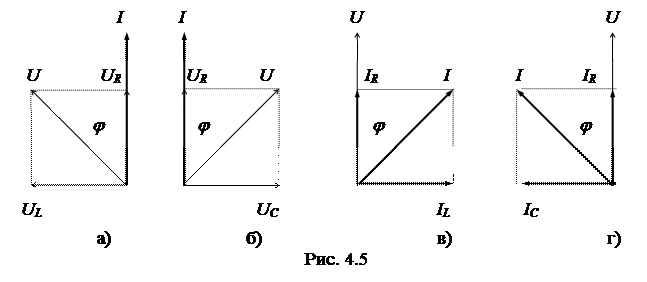
Векторные диаграммы токов и напряжений для схемы с последовательным соединением элементов R, L и R, C показаны на рис. 4.5а, б, а для схемы с параллельным соединением - на рис. 4.5в, г.
При выполнении расчетной части работы внутреннее активное сопротивление катушки Ro не учитывается и принимается равным нулю. В реальных исследуемых цепях наличие небольшого сопротивления Ro приведет к уменьшению угла j между напряжением и током катушки по сравнению с его расчетным значением, что и будет зафиксировано измерительным прибором.
4.4. Расчетная часть
1. Выполнить расчет схемы с последовательным соединением резистора R и катушки L (рис. 4.1). Определить ток I, напряжения на отдельных элементах UR и UL, углы сдвига фаз между отдельными напряжениями и током (j, j1, j2) . Результаты расчета внести в табл. 4.2.
2. Выполнить расчет схемы с последовательным соединением резистора R и конденсатора C (рис. 4.2). Определить ток I, напряжения на отдельных элементах UR и UC, углы сдвига фаз между отдельными напряжениями и током (j, j1 ,j 2) . Результаты расчета внести в табл. 4.2.
3. Выполнить расчет схемы с параллельным соединением резистора R и катушки L (рис. 4.3). Определить ток источника I, токи в отдельных элементах IR и IL, углы сдвига фаз между ЭДС источника и отдельными токами (j, j1, j2). Результаты расчета внести в табл. 4.3.
4. Выполнить расчет схемы с параллельным соединением резистора R и конденсатора C (рис. 4.4). Определить ток источника I, токи в отдельных элементах IR и IC, углы сдвига фаз между ЭДС источника и отдельными токами (j, j1, j2). Результаты расчета внести в табл. 4.3.
5. По результатам расчетов отдельно для каждой исследуемой схемы построить в выбранных масштабах векторные диаграммы токов и напряжений.
Т а б л и ц а 4.2.
| Схема | E, B | I, A | UR , B | UL , B | UC , B | j, гр | j1, гр | j2, гр |
| 1)вычис. | - | |||||||
| 1)измер. | - | |||||||
| 2)вычис. | - | |||||||
| 2)измер. | - |
Т а б л и ц а 4.3
| Схема | E, B | I, A | IR, A | IL, A | IC, A | j, гр | j1, гр | j2, гр |
| 3)вычис. | - | |||||||
| 3)измер. | - | |||||||
| 4)вычис. | - | |||||||
| 4)измер. | - |
4.4. Экспериментальная часть
1. Собрать электрическую цепь по схеме рис. 4.6. Установить заданные значения параметров отдельных элементов ( 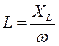 ). Измерить ток в цепи I, напряжения на отдельных участках цепи U, UR и UL, углы сдвига фаз между отдельными напряжениями и током (j, j1, j2). Результаты измерений внести в табл. 4.2.
). Измерить ток в цепи I, напряжения на отдельных участках цепи U, UR и UL, углы сдвига фаз между отдельными напряжениями и током (j, j1, j2). Результаты измерений внести в табл. 4.2.
2. Собрать электрическую цепь по схеме рис. 4.7. Установить заданные значения параметров отдельных элементов ( 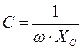 ). Измерить ток в цепи I, напряжения на отдельных участках цепи U, UR и UC, углы сдвига фаз между отдельными напряжениями и током (j, j1, j2). Результаты измерений внести в табл. 4.2.
). Измерить ток в цепи I, напряжения на отдельных участках цепи U, UR и UC, углы сдвига фаз между отдельными напряжениями и током (j, j1, j2). Результаты измерений внести в табл. 4.2.
3. Собрать электрическую цепь по схеме рис. 4.8 и 4.10. Установить заданные значения параметров отдельных элементов ( 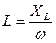 ). Измерить напряжение U и ток I источника, токи в отдельных ветвях IR и IL, углы сдвига фаз между напряжением источника и отдельными токами (j, j1, j2). Результаты измерений внести в табл. 4.3.
). Измерить напряжение U и ток I источника, токи в отдельных ветвях IR и IL, углы сдвига фаз между напряжением источника и отдельными токами (j, j1, j2). Результаты измерений внести в табл. 4.3.
4.
 |
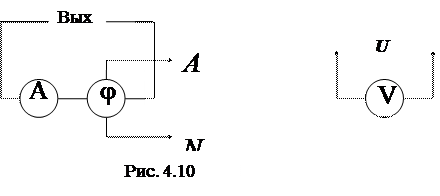 |
4. Собрать электрическую цепь по схеме рис. 4.9 и 4.10. Установить заданные значения параметров отдельных элементов ( 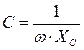 ). Измерить напряжение U и ток I источника, токи в отдельных ветвях IR и IС, углы сдвига фаз между напряжением источника и отдельными токами (j, j1, j2). Результаты измерений внести в табл. 4.3.
). Измерить напряжение U и ток I источника, токи в отдельных ветвях IR и IС, углы сдвига фаз между напряжением источника и отдельными токами (j, j1, j2). Результаты измерений внести в табл. 4.3.
4.5. Анализ результатов работы
1. Сравнить количественные результаты измерений с аналогичными данными расчета. Если численные значения одной и той же физической величины (тока или напряжения), полученные расчетным и экспериментальным путем, отличаются более чем на 10%, следует установить ошибку в Ваших действиях и ее устранить.
2. Проверить численный баланс токов в узлах согласно 1-у закону Кирхгофа и баланс напряжений в контурах согласно 2-у закону Кирхгофа.
4.7. Содержание отчета
Отчет по данной лабораторной работе должен содержать:
1) титульный лист по стандартной форме;
2) цель работы;
3) исходные данные (эквивалентные схемы исследуемых цепей и параметры их элементов);
4) таблицы с результатами вычислений и измерений;
5) основные расчетные формулы и уравнения;
6) векторные диаграммы токов и напряжений;
7) выводы и заключение о степени соответствия расчетных и экспериментальных результатов.
Контрольные вопросы
1. Что такое активное сопротивление элемента цепи? Тождественны ли понятия активное и омическое сопротивление проводника?
2. Что такое реактивное сопротивление элемента цепи? Как определяются реактивные сопротивления катушки и конденсатора?
3. Что такое полное сопротивление? Как определить полное сопротивление каждой из исследуемых схем?
4. Что такое угол сдвига фаз?
5. Составьте уравнения по 1-му закону Кирхгофа для схем рис. 4.2 и уравнения по 2-му закону Кирхгофа для схем рис. 4.1.
Л а б о р а т о р н а я р а б о т а № 11
ИССЛЕДОВАНИЕ ТРЕХФАЗНОЙ ЦЕПИ ПРИ СОЕДИНЕНИИ
НАГРУЗКИ ЗВЕЗДОЙ С НУЛЕВЫМ ПРОВОДОМ
11.1.Цель работы
1. Изучение методов расчета схемы трехфазной цепи, соединенной звездой с нулевым проводом.
2. Исследование влияния симметрии и характера нагрузки на симметрию линейных (фазных) токов и ток в нулевом проводе.
3. Построение векторных диаграмм токов и напряжений для трехфазной цепи.
11.2. Исходные данные
Заданы:
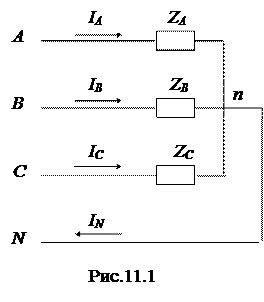
1. Эквивалентная схема исследуемой трехфазной цепи с нагрузкой, соединенной звездой с нулевым проводом (рис. 11.1). На входе схемы действует симметричный трехфазный генератор с напряжением Uл / Uф = 127/73В.
2. Комплексные сопротивления фаз для 4 типов нагрузки:
1) симметричная нагрузка RА = RВ = RС = Rф;
2) несимметричная однородная нагрузка RА ¹ RВ ¹ RС;
3) несимметричная неоднородная нагрузка ZА=RА, ZВ=RВ+jXВ, ZC=RС+jXС (табл. 11.1).
3. Рабочая схема исследуемой цепи и схемы включения измерительных приборов (рис. 11.2).
 |
Т а б л и ц а 11.1
| Вариант | ||||||||||
| 1)Rф, Ом | ||||||||||
| 2)RА, Ом | ||||||||||
| RВ , Ом | ||||||||||
| RС , Ом | ||||||||||
| 3)RА, Ом | ||||||||||
| RВ, Ом | ||||||||||
| ХВ, Ом | -50 | -72 | -45 | -69 | -68 | |||||
| RС, Ом | ||||||||||
| ХС, Ом | -42 | -62 | -69 | -58 | -66 |
11.3.Теоретические сведения и методические указания
Симметричный трехфазный генератор обеспечивает на выходе два уровня напряжения - линейное UЛ и фазное Uф, соотношение между которыми составляет UЛ/Uф= 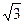 . В промышленных условиях номинальное напряжение трехфазного генератора UЛ/Uф=380/220В, в лаборатории ТОЭ уровень этого напряжения снижен по соображениям техники безопасности до UЛ/Uф=127/73В. Наличие двух уровней напряжения в трехфазном генераторе позволяет подключать к нему приемники с различными номинальными напряжениями, что обеспечивается способом соединения фаз приемника между собой. Если отдельные фазы приемника рассчитаны на фазное напряжение генератора, то они соединяются по схеме звезды (с нулевым проводом или без него).
. В промышленных условиях номинальное напряжение трехфазного генератора UЛ/Uф=380/220В, в лаборатории ТОЭ уровень этого напряжения снижен по соображениям техники безопасности до UЛ/Uф=127/73В. Наличие двух уровней напряжения в трехфазном генераторе позволяет подключать к нему приемники с различными номинальными напряжениями, что обеспечивается способом соединения фаз приемника между собой. Если отдельные фазы приемника рассчитаны на фазное напряжение генератора, то они соединяются по схеме звезды (с нулевым проводом или без него).
При наличии нулевого провода симметрия фазных напряжений на приемнике диктуется генератором и не зависит от характера нагрузки: UА=Uф·ej0, UB=Uф·e -j120, UC=Uф·e j120. Линейные (фазные) токи для каждой фазы определяются по закону Ома: 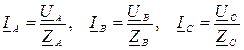 , а ток в нулевом проводе - по 1-му закону Кирхгофа: IN = IА +IB + IC.
, а ток в нулевом проводе - по 1-му закону Кирхгофа: IN = IА +IB + IC.
При симметричной нагрузке ток в нулевом проводе равен нулю, нулевой провод не влияет на режим цепи и может быть удален. При несимметричной нагрузке векторная сумма токов фаз не равна нулю, нулевой провод при этом обеспечивает на фазах нагрузки симметричное напряжение источника.
Для измерения токов в нескольких ветвях цепи применяется коммутатор токовых цепей, позволяющий включать приборы (амперметр, фазометр) поочередно в любую ветвь цепи.
Показание фазометра равно углу сдвига фаз между вектором напряжения U = U·eja и вектором тока I = I·ejb, которые подведены к обмоткам прибора, т.е. j = a - b. Если к фазометру подведен базовый вектор напряжения UО=U·e j0 с начальной фазой, равной нулю, и измеряемый вектор тока I = I·ejb, то показание фазометра будет численно равно начальной фазе (аргументу) вектора тока со знаком минус, т.е. j = 0 - b = -b. В качестве базового вектора напряжения принимается фазное напряжение фазы А генератора UО=UА=Uф·ej0.
11.4. Расчетная часть
1. Произвести расчет схемы трехфазной цепи для каждого из заданных видов нагрузки (п. 1, 2, 3) в комплексной форме. В результате расчета определить линейные (фазные) токи IА, IB, IС и ток в нулевом проводе IN. Результаты расчета записать в виде комплексных чисел ( I = I×eja ) в табл. 11.2.
2. Определить активные мощности каждой из фаз РА, РB, РС и мощность всей цепи РS. Результаты расчета записать в табл. 11.3
3. По результатам расчета для каждого вида нагрузки построить векторные диаграммы токов и напряжений.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|