Преподаватель - Брыкало А.А.. Конспект урока «Математика». Ход урока

Преподаватель - Брыкало А.А.

brukalo_aa@mail.ru

https://vk.com/id399759339

Конспект урока «Математика»

Дата13.05.2020

Группа88профессия«Тракторист-машинист с/х производства» курс2

Тема 132-133:Практическое занятие №71 «Первообразная и интеграл»

Форма работы:индивидуальная, электронное обучение

Тип урока:урок совершенствования знаний, умений и навыков

Продолжительность урока: 2 часа

Цель урока:корректировать знания, умения и навыки по теме «Первообразная и интеграл», закрепить и систематизировать знания по данной теме.

Используемая литература:

Учебник: Математика. Алгебра и начала математического анализа. 10-11 классы: учебник для общеобразовательных организаций: базовый и углубленные уровни./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение, 2018г

Интернет-ресурсы:

Методика преподавания математики http://methmath.chat.ru/

Ход урока

Организационный этап:

Мотивационный модуль

Ребята, на этом уроке вы повторите материал по теме «Первообразная и интеграл», выполните практическую работу.

Основная часть:

Объясняющий модуль

Теоретический материал для самостоятельного изучения

1. Повторите теоретический материал.

1. Первообразная

Определение 1. Функцию F (x) , определенную на интервале (a, b), называют первообразной функции f (x) , определенной на интервале (a, b), если для каждого 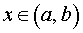выполнено равенство F' (x) = f (x) .

Например, из справедливости равенства (sin 2x)' = 2 cos 2x вытекает, что функция F (x) = sin 2x является первообразной функции f (x) = 2 cos 2x .

Замечание. Функция F (x) = sin 2x не является единственной первообразной функции f (x) = 2 cos 2x , поскольку функция F (x) = sin 2x + 10 , или функция F (x) = sin 2x – 3 , или функции вида F (x) = sin 2x + c , где c – любое число, также являются первообразными функции f (x) = 2 cos 2x .

Справедлива следующая теорема, доказательство которой выходит за рамки школьного курса математики.

Теорема 1. Если функция F (x) является первообразной функции f (x) на интервале (a, b) , то любая другая первообразная функции f (x) на интервале (a, b) имеет вид F (x) + с , где c – некоторое число.

2. Неопределенный интеграл

Определение 2. Множество всех первообразных функции f (x) называют неопределенным интегралом от функции f (x) и обозначают

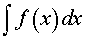
(1)

Обозначение (1) читается так: «Неопределенный интеграл от функции f (x) по dx» .

Если F (x) является первообразной f (x) , то в силу теоремы 1 смысл формулы (1) заключается в следующем:

(2)

Однако для упрощения формулу (2) принято записывать в виде

(3)

подразумевая, но не указывая специально, что c – любое число.

В формуле (3) функцию f (x) называют подынтегральной функцией, выражение f (x) dx называют подынтегральным выражением, а число c называют постоянной интегрирования.

Операцию вычисления (взятия) интеграла по известной подынтегральной функции называют интегрированием функции.

3. Правила интегрирования. Замена переменной в неопределенном интеграле

Вычисление интегралов (интегрирование) основано на применении следующих правил, которые непосредственно вытекают из правил вычисления производных.

Правило 1 (интеграл от произведения числа на функцию). Справедливо равенство

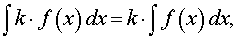
где k – любое число.

Другими словами, интеграл от произведения числа на функцию равен произведению этого числа на интеграл от функции.

Правило 2 (интеграл от суммы функций). Интеграл от суммы функций вычисляется по формуле

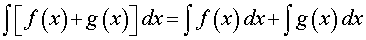
то есть интеграл от суммы функций равен сумме интегралов от этих функций.

Правило 3 (интеграл от разности функций). Интеграл от разности функций вычисляется по формуле

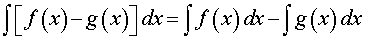
то есть интеграл от разности функций равен разности интегралов от этих функций.

Правило 4 (интегрирование при помощи замены переменной). Из справедливости формулы

вытекает, что

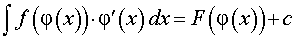
(4)

если все входящие в формулу (4) функции f (φ (x)), φ' (x), F (φ (x)) определены.

Пример 1.

Значение первообразной F (x) функции f (x) = – 4 sin x в точке x = 0 равно 9. Найти .

Решение.

Поскольку

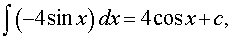
то F (x) = 4 cos x + c,

(6)

Подставляя в формулу значение x = 0 , находим значение постоянной интегрирования c:

F (0) = 4 cos 0 + c = 9,

4 + c = 9, c = 5.

Следовательно,

F (x) = 4 cos x + 5

Поэтому

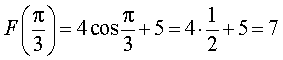
Ответ. 7

Выполнение практической части работы

2.Оформление работы:

Практическое занятие № 71

Тема: «Первообразная и интеграл»

Цель: корректировать знания, умения и навыки по теме «Первообразная и интеграл», закрепить и систематизировать знания по данной теме.

Практическая часть работы:

1. Вычислить неопределенный интеграл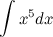

2. Вычислить неопределенный интеграл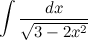

3. Является ли функция F(x)=х² первообразной для функции f(x) = 2х

4. Для функции f(x) = 4 – х² найти первообразную, график которой проходит через точку (-3; 10).

5. Найти площадь фигуры, ограниченную графиками функций y =2x-x² и x+y=0.

Домашнее задание:

Оформить отчет по практической работе