
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Цвында О.. Вариант №1
Цвында О.
Вариант №1
1.Сколько различных слов можно получить перестановками всех букв в слове ЭКЗАМЕН?
7 букв всего, значит 7!=1*2*3*4*5*6*7=5040
Ответ: 5040 различных слов можно получить перестановками всех букв
2.В ящике 6 белых и 8 чёрных шаров. Из ящика вынули 2 шара (не возвращая вынутый шар в ящик). Какова вероятность того, что оба шара белые?
Решение:
P(AB) =P(A)*P(B/A)
P(A)=6/14=3/7
P(B/A)=(6-1)/(8+6-1)=5/13
P(AB)=3/7*5/13=15/91=0,165
Ответ: вероятность того, что оба шара белые 15/91 или 0,165
3.Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,55, а для второго – 0,65. Найти вероятность того, что при одном залпе в мишень попадает только один стрелок.
Решение:
p1=0,55
p2=0,65
q1=0,45
q2=0,35
Р(А)=p1q2+q1p2=0,55*0,35+0,45*0,65=0,1925+0,2925=0,485
Ответ: вероятность того, что при одном залпе в мишень попадает только один стрелок 0,485
4.Монету бросают 7 раз. Найти вероятность того, что 4 раза она упадёт гербом вверх.
Решение:
2^7=128
7!/(4!*2!)=7*6*5/2=106
105/128=0,82
Ответ: вероятность того, что 4 раза она упадёт гербом вверх 0,82
5.Имеется четыре ящика. В первом ящике 3 белых и 4 чёрных шара, во втором – 5 белых и 3 чёрных шара, в третьем – 3 белых и 6 чёрных шаров, в четвёртом – 5 белых и 8 чёрных шаров. Выбирают наугад один из ящиков и вынимают из него шар. Найти вероятность того, что этот шар белый.
Решение:
в первом ящике 3 белых шара, всего их там 3+4=7, то вероятность того чтобы из первого достали белый шар равна 3/7, во втором ящике 5 белых, а всего 5+3=8, то вероятность что из второго ящика достанут белый шар равна 5/8, в третьем ящике 3 белых шара, всего их там 3+6=9, то вероятность того чтобы из первого достали белый шар равна 3/9=1/3, в четвёртом ящике 5 белых, а всего 5+8=13, то вероятность что из второго ящика достанут белый шар равна 5/13.
3/7*5/8*1/3*5/13=0,43*0,625*0,33*0,385=0,341
Ответ: вероятность того, что этот шар белый 0,341
6. Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины X, заданной законом распределения:
| X | -3 | |||
| p | 0,4 | 0,3 | 0,1 | 0,2 |
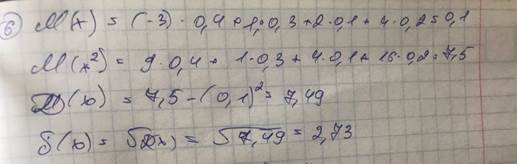
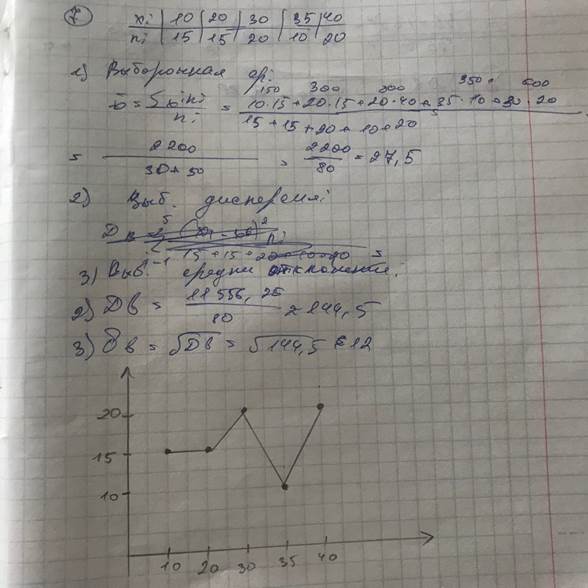
7. Найти выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение. Построить полигон частот по данному распределению выборки:
| xi | |||||
| ni |
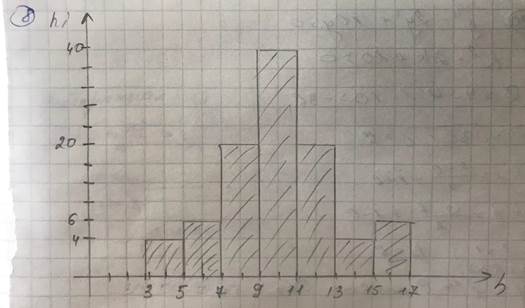
8. Построить гистограмму частот по данному распределению выборки:
| Частичный интервал длиной h | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 |
| Сумма частот вариант частичного интервала ni |
9. Мода вариационного ряда 2; 3; 4; 8; 9; 9; 10 равна 9
10. Бросают 2 игральные кости. Вероятность того, что выпадет не менее 11 очков, равна 1/12
11. Найти наибольшее и наименьшее значения функции 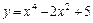 на отрезке [-2; 2].
на отрезке [-2; 2].
Min (-1,4);(1;4)
Max (0;5)
12. Найдите максимум функции 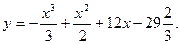
Max(4;5)
13. Вычислите определитель 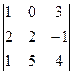 .
.

14. Если 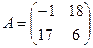 и
и 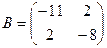 , то матрица C=A-B имеет вид …
, то матрица C=A-B имеет вид …
15. Значение предела 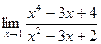 равно 1) 1 2) 2 3) -2 4)-1 5) 3
равно 1) 1 2) 2 3) -2 4)-1 5) 3
16. Характеристическое уравнение для уравнения 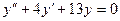 имеет вид
имеет вид
1) 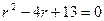 2)
2) 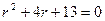 3)
3) 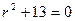 4)
4) 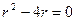 5)
5) 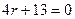
17. Найти общее решение уравнения 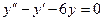 .
.
1) 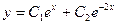 2)
2) 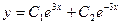 3)
3) 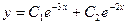
4) 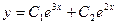 5)
5) 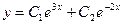
18. Укажите первообразную функции 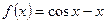 .
.
1) 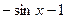 2)
2)  3)
3) 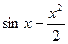 4)
4) 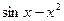
19. Найдите угловой коэффициент касательной, проведенной к графику функции 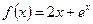 в его точке с абсциссой
в его точке с абсциссой 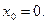
1) 1 2) -5 3) -1 4) 5 5) 2 6) 3 7) 0 8) -2
20. Решить уравнение 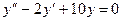 .
.

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|